对几类思维训练题分析与解答
这个学期我们三年级关于思维训练重点练习了以下五种类型。孩子们对有些题型理解起来还有一定难度,现在简单分析讲解如下,供家长辅导和孩子们学习时进行参考。
题型一:填一填□里该填几。
例1.□71÷5,要使商是两位数,□可以填的数是( )。
分析:这是一道三位数除以一位数的题目,要使商是两位数,被除数的百位上的数要比除数小,也就是被除数的最高位要填比5小的数,比5小的数有0、1、2、3、4,因为一个整数的最高位不能为0,所以符合条件的数是1、2、3、4。又因为题目要求的是可以填的数是几,因此只要填符合条件的一个数即可。如果都填要用顿号隔开。
解答:□71÷5,要使商是两位数,□可以填的数是( 1 )。
练一练。
1、□28÷7,要使商是三位数,□可以填的数是( )。
2.□60÷4,要使商是两位数,□最大填( )。
3.□49÷3,要使商是三位数,□最小填( )。











例2.□54÷6,要使商的中间0,□可以填的数是( )。
分析:要使商的中间有0,被除数百位上的除以除数应该没有余数,也就是说正好是除数的整倍数,十位上的数除以除数不够除。这道题除数是6,被除数的百位只能是6。
解答:□54÷6,要使商的中间0,□可以填的数是( 6 )。
练一练。
1.□44÷6,要使商的中间0,□可以填的数是( )。
2.3□4÷6,要使商末尾有0,□可以填的数是( )。












题型二:猜一猜图形表示的数是多少。
例:(35+□)×3=225, □=( )
分析:观察算式能知道(35+□)是一个因数,3是另一个因数,225是它们的积。可以先根据“一个因数=积÷另一个因数”,求出35+□的和,即225÷3=75,在根据“一个加数=和-另一个加数”求出□表示的数,即75-35=40。
解答:(35+□)×3=225, □=(40 )
练一练。
1. 58+76-□=120, □=( )
2. ○×9+20=200, ○=( )
3. □÷4+33=87, □=( )
4. 90-□÷5=81, □=( )












题型三:和倍、差倍问题
例1、一套成人服装630元,上衣的价钱是裤子的2倍,一件上衣和一条裤子各多少钱?
分析:这是和倍问题。解答和倍应用题的关键是找出两数的和以及与其对应的倍数和。要想顺利解决和倍应用题,最好的方法就是根据题意,画出线段图,使数量关系一目了然,从而正确的列式计算。
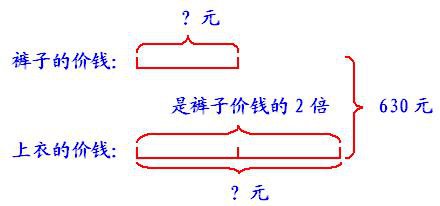
从线段图能看出,630是一件上衣和一条裤子的价钱的和,上衣是2倍数,裤子是1倍数。上衣和裤子一共是3倍数,630对应的倍数和就是(2+1),要求1倍数就应该用630÷3=210(元),210元是一条裤子的价钱,再用210×2=420(元)就是一件上衣的价钱。
解答:2+1=3 综合算式:630÷(2+1)
630÷3=210(元) =630÷3
210×2=420(元) =210(元)
210×2=420(元)
答:一件上衣420元,一条裤子210元。
练一练。
1、学校有科技书和故事书共480本科技书的本数是故事书的3倍,两种书各多少本?
2、一个养鸡场有675只鸡,其中母鸡是公鸡的4倍,这个养鸡场有公鸡、母鸡各多少只?












例2、今年爸爸的年龄是小华的4倍,爸爸比小华大36岁。爸爸和小华各多少岁?
分析:这是差倍问题。解答和倍应用题的关键是找出两数的差以及与其对应的倍数差。要想顺利解决差倍问题,也和和倍问题一样根据题意,画出线段图,从而正确的列式计算。
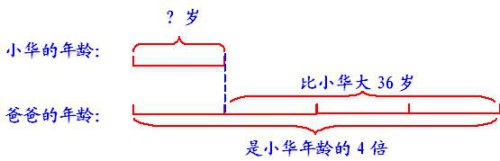
从线段图上能看出36是爸爸比小华大的岁数,也就是年龄差。爸爸的年龄是4倍数,小华的年龄是1倍数,倍数差是(4-1)。要求一倍数(小华的年龄)就用36÷3=12(岁),再用12×4=48(岁)求出爸爸的年龄。
解答:4-1=3 综合算式:36÷(4-1)
36÷3=12 (岁) =36÷3
12×4=48 (岁) =12(岁)
12×4=48(岁)
答:爸爸今年48岁,小华12岁。
练一练
1、一大盒比一小盒水彩笔多36支,大盒里的支数是小盒的2倍。大盒和小盒各装了多少支彩笔?
2、一张桌子比一把椅子贵280元,一张桌子的价钱是一把椅子的3倍,桌子和椅子的单价分别是多少元?












题型四:
例1:一桶水连桶称重60千克,用去一半后,连桶称还重32千克。这桶水有水多少千克?空桶重多少千克?
分析:根据题意可以知道60千克是空桶和一桶水的重量,32千克是空桶和半桶水的重量,可以列出下面的关系式:
空桶重+一桶水重=60千克 ①
空桶重+半桶水重=32千克 ②
思路一:用①-②=半桶水的重量,就是60-32=28(千克),半桶水的重量×2能求出一桶水的重量,即28×2=56(千克),再求出空桶的重量60-56=4(千克)或32-28=4(千克)。
思路二:用②×2求出两个空桶的重量+一桶水的重量,即32×2=64(千克),再用64-60=4(千克)求出空桶的重量,接着用60-4=56(千克)求出一桶水的重量。
解答:
方法一: 60-32=28(千克)
水 重:28×2=56 (千克)
空桶重:60-56=4(千克)或32-28=4(千克)
方法二: 32×2=64(千克)
空桶重:64-60=4(千克)
水 重:60-56=4(千克)
练一练
1.一筐苹果连筐重80千克,吃去一半后,连筐重42千克。这筐苹果有多少千克?筐重多少?
2.一桶油连桶共重92千克,用去一半油后,连桶共重52千克。桶和油各重多少千克?












题型五:长方形正方形周长与面积的延伸。
例1、把一张长12厘米、宽8厘米的长方形纸上剪下一个最大的正方形,它的面积是多少平方厘米?剩下图形的面积是多少平方厘米?
分析:根据题意在这个长方形中剪下的最大正方形边长应该是8厘米,那么它的面积因该是8×8=64(平方厘米)。剩下图形的面积有两种思路:用原来长方形的面积减去剪下正方形的面积,还可以求出剩下图形的宽,用长方形面积公式求出它的面积。(如下图)
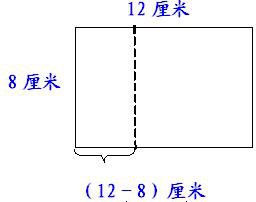
解答:
剪下最大正方形的面积: 剩下图形的面积:
8×8=64(平方厘米) 12×8=96(平方厘米)
96-64=32(平方厘米)
或:12-8=4(厘米)
8×4=32(平方厘米)
答:剪下一个最大的正方形的面积是64平方厘米,
剩下图形的面积是32平方厘米。
练一练
1.从一张长是14厘米、宽是9厘米的长方形纸上剪下一个最大的正方形,剩下的部分是多少平方厘米?
2.把一张边长10厘米的正方形纸,剪下一个长10厘米、宽8厘米的长方形。剩下的部分是什么图形?它的面积是多少?
3.把一张长8厘米、宽6厘米的长方形纸上剪下一个最大的正方形,它的周长是多少厘米?
以上是我对一些思维问题的讲解,不知是否对家长和学生学习有所帮助,如果有所帮助,那是我最想看到的。