第二十二章:图的基本算法关于此章节的习题解答,请查阅 :https://sites.google.com/site/algorithmssolutio
第二十二章:图的基本算法
关于此章节的习题解答,请查阅 :https://sites.google.com/site/algorithmssolution/home/c22
一、图的概念
图的分类: 是否有环是否有重边是否有有向边Simple Undirected Graph(简单无向图)×××Multigraph(多重图)×√×Pseudograph(伪图)√√×Simple Directed Graph(简单有向图)××√Directed Multigraph(有向多重图)√√√Mixed Graph(混合图)√√有向边和无向边共存
Infinite Graph:有无限个点的图。
Finite Graph:有有限个点的图。
MultiEdge:重边。
Isolated Vertex:度数为0的点。
Pendant Vertex:度数为1的点。
完全图(Kn):任意两个点之间都有一条边。
注意点:1、小的图通常用邻接矩阵。2、一般的图算法都是用邻接表。3、邻接表的存储空间为O(V+E)。4、邻接矩阵存储空间为O(V^2)。5、对于无向图,如果用邻接矩阵存储,则可以只存储主对角线和主对角线以上的部分,可以节约一般空间。6、有向边用(u,v)表示,无向边用{u,v}表示。7、如果是加权图,则邻接表表示可以在邻接表的每个节点中加一个weight,而邻接矩阵可以在单元格的位置用权值替代。8、无向图中一个环有两个度。9、无向图中sum(deg(v))=2e,因此度数之和一定是偶数,如果给定度数序列之和为奇数,则肯定不是无向图。10、有向图中sum(deg-(v))=sum(deg+(v))=|E|。
对于邻接表表示有一点要注意:如果A与B、C、D相连,则A的邻接表的顺序是不定的,可能是D、C、B,也可能是C、D、B。
以下是树的概念,但是后面DFS、BFS生成深度优先树和广度优先树时会用到:
v的祖先:包括v和v的真祖先。v的
真祖先:如果存在u(不含v),使得u到v存在一条路径,则u为v的真祖先。v的
后裔:包括v和v的真后裔。v的
真后裔:如果存在u(不含v),使得v到u有一条路径,则u为v的真后裔。
强连通图:任意两个顶点u,v,u到v和v到u都有路径。
弱连通图:此图为有向图,他不是强连通图,但是如果把有向边变成无向边后,图为连通的,则此图为弱连通图。
二分图(Bipartite Graph):如果一个图的点集能被分成两个不相交的子集V1、V2,使得每条边都是V1中的点与V2中的点连接。
完全二分图:点集分为两个子集后,每个子集中任意抽一个点,他们之间都有边。
着色定理:如果图是二分图当且仅当给图中每个点赋予红蓝两色之一,使得没有一条边的两个顶点是同一个颜色。着色定理可以通过BFS来实现,即距离为奇数的顶点着色为蓝色,偶数的顶点着色为红色,着色完毕需要O(V+E),然后在遍历每条边,检查是否着色正确,O(V+E)。定理:图是二分图当且仅当不可能从某个顶点开始走,经过奇数条边又回到起点。
割点:如果去掉某个点,连通分支数增加,则此点为割点。
割边(桥):如果去掉某个边,连通分支数增加,则此边为割边。
欧拉回路:在图中能找到遍历每条边一次的简单回路(注意是简单回路);
欧拉路径:在图中能找到遍历每条边一次的简单路径;
在无向图中,图中有欧拉回路当且仅当图中每个顶点的度数为偶数;在有向图中,图中有欧拉回路当且仅当图中每个顶点出度和入度相同;
在无向图中,图中有欧拉路径当且精当图中只有两个顶点度数为奇数;在有向图中,图中有欧拉路径当且仅当图中只有两个点,出度入度相差奇数;
汉密尔顿回路:在图中能找到能遍历每个点一次的简单回路;
汉密尔顿路径:在图中能找到能遍历每个点一次的简单路径;
连通分支:连通的点的集合,比如{A,B,C}为图的一个连通分支;
在无向图中判断是否存在回路:|E|>|V|-1且连通图,则一定有回路。在有向图中判断是否存在回路:DFS有反向边。
二、BFS用途:(1)遍历图。(2)在图的每条边的权值都为1的前提下,计算最短路径。
注意点:(1)任意一条边(u,v),d[v]<=d[u]+1;(2)在队列中,设队头为u,队尾为v,d[v]<=d[u]+1;
最最重要的一点:BFS能够生成最短路径树,但是并不是所有的最短路径树都能够通过BFS生成。例如:
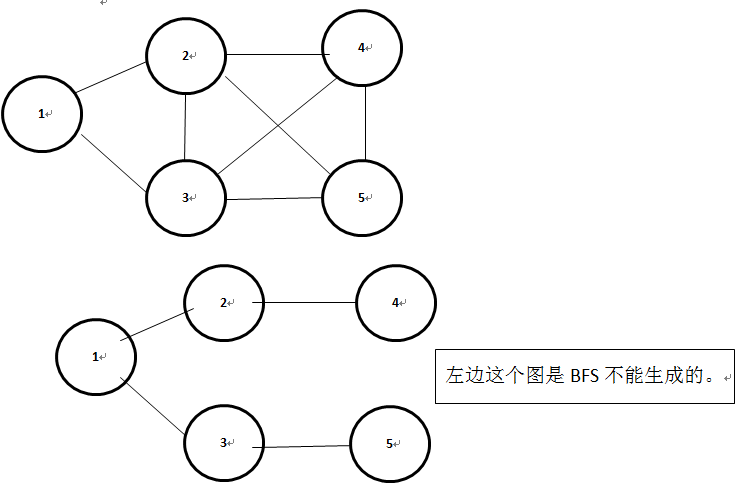 三、DFS
三、DFS
树边:深度优先树中出现的边。
正向边:u到非直接后裔的边。
反向边:u到祖先(包括自己)的边。
交叉边:u和v不是祖先后裔关系。
在无向图中,只有树边和反向边。
四、拓扑排序如果存在(u,v),则f[u]>f[v].
拓扑排序有两种实现:(1)按f[]降序DFS。(2)每次删除一个入度为0的点。
