栈和队列

栈和队列是特殊的线性表。

栈

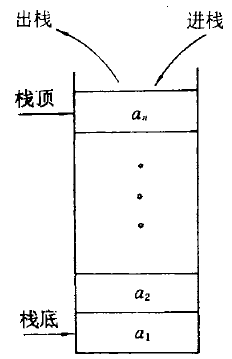
栈（stack）是限定在表尾进行插入或删除操作的线性表，表尾端称为栈顶（top），表头端称为栈底（bottom），不含元素的栈称为空栈。

栈是后进先出（last in first out，LIFO）。

栈的抽象数据定义：

?

ADT{  数据对象：D  数据关系：R1  基本操作：  initStack(&S)    操作结果：构造一个空栈S  destroyStack(&S)    初始条件：栈S已存在    操作结果：栈S被销毁  clearStack(&S)    初始条件：栈S已存在    操作结果：栈S被清空  stackEmpty(&S)    初始条件：栈S已存在    操作结果：若S为空栈，则返回TRUE，否则返回FALSE  stackLength(&S)    初始条件：栈S已存在    操作结果：返回S的元素个数  getTop(&S,e)    初始条件：栈S已存在，且非空    操作结果：用e返回S的栈顶元素  push(&S,e)    初始条件：栈S已存在    操作结果：插入元素e为新的栈顶元素  pop(&S,e)    初始条件：栈S已存在且非空    操作结果：删除S的栈顶元素，并用e返回其值  stackTraverse(&S,visit())    初始条件：栈S已存在    操作结果：使用visit函数遍历栈S}ADT Stack

?栈的表示和实现

栈有两种表示方法：顺序栈和链式栈

顺序栈即栈的顺序存储结构式利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同事附设指针top指示栈顶元素在顺序栈中的位置。

栈的初始化操作为：

? 按设定的初始分配量进行第一次存储分配，base可称为栈底指针，在顺序栈中，它始终指定栈底的位置，若base的值为NULL，则表明栈结构不存在，称top为栈顶指针，其初值指向栈底，即top=base作为栈空的标记，当新元素进栈时，top+1，删除栈顶元素时，top-1，非空栈中的栈顶指针始终在栈顶元素的下一个位置上。

?

栈的C语言表示：

#include <stdio.h>#include <stdlib.h>#define TRUE 1#define FALSE 0 #define STACK_INIT_SIZE 5typedef int elemType;typedef struct sqStack{elemType *base;elemType *top;int length;int maxSize;}sqStack;/*初始化一个栈*/void initStack(sqStack *S){elemType *p = malloc(STACK_INIT_SIZE * sizeof(elemType));if(!p){printf("空间分配失败!\n");exit(0);}else{printf("空间分配成功!\n");S->length = 0;S->maxSize = STACK_INIT_SIZE;S->base = S->top = p;}}/*清空一个栈*/void clearStack(sqStack *S){S->length = 0;S->top = S->base;}/*销毁一个栈*/void destroyStack(sqStack *S){clearStack(S);free(S->base);S->base = S->top = NULL;S->maxSize = 0;}/*判断一个栈是否为空*/int stackEmpty(sqStack *S){return S->top == S->base ? 1 : 0;}/*获取栈中元素的个数*/int stackLength(sqStack *S){return S->length;}/*用e返回栈顶元素*/void getTop(sqStack *S,elemType e){if(S->base == S->top){printf("该栈已空!\n");exit(0);}else{e= *--(S->top);}}/*向栈顶插入元素e*/void push(sqStack *S,elemType e){if(S->top - S->base == S->maxSize){elemType *p = realloc(S->base,(S->maxSize+1)*sizeof(elemType));if(!p){printf("空间分配失败!\n");exit(0);}else{printf("空间再分配成功!\n");  S->maxSize++;S->base = p;S->top = S->base + S->length;}}S->length++;*(S->top) = e;S->top++;}/*删除栈顶元素，并用e返回其值*/elemType pop(sqStack *S){if(S->base == S->top){printf("该栈已空!\n");exit(0);}else{S->length--;return *(--S->top);}}/*遍历栈*/void stackTraverse(sqStack *S,void (*visit)(elemType)){if(S->base == S->top){printf("\n该栈已空!\n");exit(0);}else{elemType *p= S->top;while(S->base!=p){p--;visit(*p);}}}void visit(elemType e){printf("%d ",e);}int main(){sqStack S;initStack(&S);int i;for(i=1;i<=6;i++){push(&S,i*2);}stackTraverse(&S,visit);elemType e = pop(&S);printf("\npop操作取得的值是:%d\n",e);stackTraverse(&S,visit);clearStack(&S);stackTraverse(&S,visit);return 0;}

?