近年考研概率统计数学三题型解析二

2013-12-13

近年考研概率统计数学三题型解析二读书人网最新精心整理推荐，望读者定期关注。

　　题型一：分布函数或密度函数性质

　　在有些考研题中，常需要利用分布函数的性质F(-∞)=0，F(∞)=1，或者密度函数的性质

进行计算或判断，如下面例题所示：

　　例1.设f1(x)为标准正态分布的概率密度，f2(x)为[-1,3]上均匀分布的概率密度，若

，(a>0, b>0) 为概率密度，则 a, b应满足( )

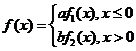
　　(A) 2a+3b=4 (B) 3a+2b=4 (C) a+b=1 (D) a+b=2 (2010年考研数学三真题第8题)

　　分析：根据密度函数的性质，只要

即可

　　解：

，所以3a+2b=4 ，选(A)

　　例2.设F1(x), F2(x)为两个分布函数，其相应的概率密度为f1(x) ,f2(x)是连续函数，则必为概率密度的是( )

　　(A) f1(x) f2(x) (B) 2f2(x) F1(x) (C) f1(x) F2(x) (D) f1(x) F2(x) +f2(x) F1(x) (2011年考研数学三真题第7题)

　　解：因为 f1(x) F2(x) +f2(x) F1(x) ≥0，且

，故选(D)

　　题型二：随机变量函数的分布

　　这类题不仅在一维随机变量考题中经常出现，而且在二维随机变量考题中也经常出现，在做这类题时，如果是连续可导函数，文都教育的老师特别提醒考生要注意变限积分的求导计算。

　　例3.设X～N(0,1),Y=X2,求Y的概率密度函数

　　解：

，FY(y)=P{Y≤y}=P{X2≤y}，当y≤0时，FY(y)=0，当y>0时，

，

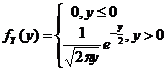
　　上面就是考研数学三概率统计部分一维随机变量及其分布的两类重要题型及解题方法，以及应特别注意的事项，供考生们参考借鉴，在以后的时间里，老师们还会陆续向考生们介绍其它常考重要题型及解题方法，希望各位考生留意查看。最后预祝各位考生在2014考研中取得佳绩。

推荐阅读：

最新考研调剂忘记密码怎样找回

读书人网为您最新整理研究生考试信息，敬请查阅，预祝各位考生顺利通过！

热点排行