1)在弯矩作用平面外有支承的构件,应根据两相邻支承点间构件段内的荷载和内力情况确定:
①所考虑构件段无横向荷载作用时:βtx =0.65+0.35M2/M1,M1和M2是在弯矩作用平面内的端弯矩,使构件段产生同向曲率时取同号,产生反向曲率时取异号,| M1|≥| M2|;
②所考虑构件段内有端弯矩和横向荷载同时作用时,使构件段产生同向曲率时,βtx =1.0;使构件段产生反向曲率时,βtx =0.85;
③所考虑构件段内无端弯矩但有横向荷载作用时:βtx =1.0。
2)弯矩作用平面外为悬臂的构件,βtx =1.0。
应用以上公式时要注意:计算采用的轴心压力和弯矩不一定是同一截面的内力值,这 与截面强度计算是不同的。
(3)局部稳定
受压翼缘板的自由外伸宽度b与其厚度t之比的限值为:
当在强度和整体稳定计算中截面塑性发展系数γx取为1.0时,上式右端可改为15
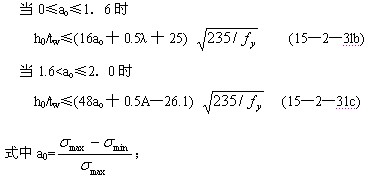
σmax——腹板计算高度边缘的最大压应力,计算时不考虑构件的稳定系数;
σmin-腹板计算高度另一边缘相应的应力,压应力取正值,拉应力取负值;
λ——构件在弯矩作用平面内的长细比;当λ<30时,取λ=30;当λ>100时,取A=1000;
箱形截面在两腹板间的受压翼缘宽厚比bo/t的限值与轴心受压时相同,见式(15-2-~24a)。腹板高厚比的限值不应超过公式(15-2-31a)或(15-2-31b)的右端乘以0.8后的 值,当此值小于40
当腹板的高厚比不能满足以上规定时,同样可以采用设置纵向加劲肋或按有效截面法 进行强度和整体稳定计算。参见轴心受压构件局部稳定计算的有关内容。
(4)刚度
压弯构件同样用控制长细比来保证刚度。有关规定参见轴心受压构件刚度计算的内容。
如果弯矩很大,则需计算因弯矩引起的挠度是否过大以至不能满足使用要求。
相关推荐: