当部件(1)~(3)正常时,系统正常,则此概率为:0.85*0.9*0.95=0.7268。
如图b时,则部件2的可靠性为:1-(1-0.8)*(1-0.85)=0.97。同样,可得部件C正常的概率为0.99则系统可靠性为:0.85×0.97×0.99=0.816。
●在对二叉树进行前序、中序和后序遍历时,最适合采用的方法是(28)。
查找树中,由根结点到所有其他结点的路径长度的总和称为(29),而(30)使上述路径长度总和达到最小,它一定是(31)。
在关于树的几个叙述中,只有(32)是正确的。
(28)A.队列操作
B.迭代程序
C.递归程序
D.栈操作
(29)A.路径和
B.深度和
C.总深度
D.内部路径长度
(30)A.丰满树
B.B+-树
C.B-树
D.穿线树
(31)A.B-树
B.平衡树
C.非平衡树
D.穿线树
(32)A.平衡树一定是丰满树
B.m阶B一树中,每个非叶子结点的后代个数≥[m/2]
C.m阶B-树中,具有k个后代的结点,必含有k-1个键值
D.用指针方式存储有n个结点二叉树,至少要有n+1个指针
答案:(28)C(29)D(30)A(31)B(32)C
解析:前序、中序和后序遍历法最适合采用递归算法来实现。查找树中,由根结点到所有其他结点的路径长度的总和称为内部路径长度,而使内部路径长度总和达到最小的树称为车满树。它必一定是平衡树,因为如果丰满树如果不是平衡树。则调整其成为平衡树后.。被调整结点高度必定减小,则内部路径长度随之减小。那么原树就不是丰满树。产生矛盾,得证。m阶B-树中,若结点含有k-1个键值,则具有k个后代。
●查找二叉树中,结点值大于左子树所有结点值,而小于右结点所有结点值。现在有一棵查找二叉树,它的结点A、B、c、D、E、F依次存放在一个起始地址为a(假定地址以字节为单位顺序编号)的连续区域中,每个结点占6个字节:前四个字节存放结点值,后二个字节依次放左指针、右指针。若该查找二叉树的根结点为D,则它的一种可能的前序遍历为(33),相应的层次遍历为(34)。在以上两种遍历情况下,结点C的左指针的存放地址为(35),它的内容为(36)。结点C的右指针的内容为(37)。
(33)A.DAFCBE
B.DFEACB
C.ADBCFE
D.DACBEF
(34)A.DAECFB
B.DFACEB
C.ABCFDE
D.DEFACB
(35)A.a+15
B.a+16
C.a+18
D.a+19
(36)A.a+6
B.a+10
C.a+14
D.a+18
(37)A.a+4
B.null
C.a+12
D.a+16
答案:(33)D(34)A(35)B(36)A(37)B
解析:可能的前序遍历为DACBEF。如图示。则其层次遍历为DAECFB。
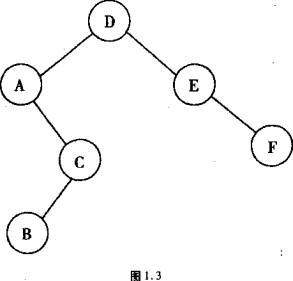
C结点左指针指向B的首地址,即为a+6。C结点左指针的地址为C的第五字节,即a+12+4=a+16。结点A的右子树为空,右指针为null。