同比增长的概念贯穿资料分析的始终，但凡涉及到计算的题目，几乎都或多或少与同比增长有关。根据其基本关系式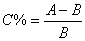
，经过出题人的精心设计，就变化出了各种各样的考题，与考生为难。涉及同比增长的计算题目有一个普遍的特点，计算式并不难列，但算起数来实在让人头疼。从基本关系式我们也可以看出，同比增长无可避免地要牵扯到百分数和除法，对计算的基本功有较高的要求。对于同比增长题目，考生首先要做到心中有数，在资料分析中出现的“增长”、“增加”、“减少”、“下降”等类似词语，除非有特殊说明，指的都是同比的增长或减少。
在这么多年的公务员考试中，计算同比增长的题目，主要有以下几种类型：
一、直接要求计算同比增长值
【例题1】：2006年国家公务员考试一卷资料分析第二题
2002年至2005年同期市保险业保费收入变化
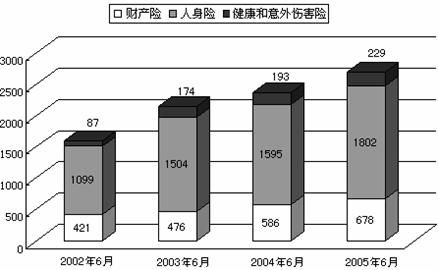
121.该市2005年6月的总保费收入比去年同期约增长了（ ）
A.14.1％ B.24.1％ C.34.1％ D.68.5％
【答案】：A。
【新东方名师贾柱保解析】：本题是典型的单纯计算同比增长类题目，只需要严格依照同比增长的计算公式代入数据就可以得到答案，注意每个月的总保费收入由三部分组成。所求同比增长为：
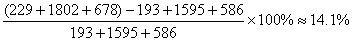
在最后的计算中，可以利用“除法首位”的估算方法，直接得到正确答案A选项。
另外，针对本题，还有一种比较简便的计算方法，就是可以用直尺分别量出代表2004年6月和2005年6月总保费的柱子高度，然后直接用高度代替报废的数额进行计算。因为所有资料分析题目中的柱状图都是用EXCEL、Origin等作图软件生成的，其几何大小与代表的数值之间均呈正比，用来计算同比增长不存在问题。
二、通过同比增长计算上年度数据
有些情况下题目中直接给出了当年统计量和同比增长的数值，而要计算的是前一年度的统计量。通过对同比增长计算式进行变形，可以得到前一年度统计量的计算式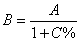
，这个式子也很重要，请考生牢记，并能够直接熟练应用。
【例题2】：2007年北京市应届大学生公务员考试资料分析第四大题
2003年，某省一次能源生产量为2223.4万吨标准煤，比上年增长6.7％，增速提高1.4个百分点，与1996年相比年均增长1.2％。多年来我省原煤产量一直在2500万吨左右徘徊，且后备资源有限，2006年原煤生产量为2760.万吨，比上年增长168.5万吨，为近年产量较高年份，原油多年来一直维持在一百多万吨的水平。2003年生产量为166.4万吨，增长9.4万吨，天燃气生产量为0.3亿立方米，增长0.1亿立方米，一次能源自给率为20.1％，已下跌至10年来最低点，其中原煤自给率为25.9％，比上年下降1.3个百分点，原油自给率仅为9.7％，下降1.7个百分点。
2003年，全省能源加工转换企业能源投入总量为8642.1万吨标准煤，比上年增长16.7％，二次能源生产总量为5359.2万吨标准煤，增长17.3％。原煤用于加工转换的总量为7902.4万吨，比上年增长14.5％，占全省原煤消费总量的74.1％，其投入量的81.2％，是作为电煤用于火力发电，产出电力1334亿千瓦时，比上年增长14.3％。
2003年全省原油加工量为1677.8万吨，比上年增长22.2％。其中：产出汽油255.2万吨，柴油434万吨，燃料油155.2万吨，液化石油气89万吨和石油制品571.2万吨，分别比上年增长16.2％、16.6％、37.2％、7％和11.9％。
131.2001年全省一次能源生产量为（ ）
A.1927.7万吨标准煤 B.1953万吨标准煤
C.1978.9万吨标准煤 D.2083.8万吨标准煤
【答案】：C。
【新东方名师贾柱保解析】：本题要求计算的甚至不是前一年度的统计量，而是向前倒推了两年，但实际计算方法没有变化。首先从材料首句可以得知2003年、2002年的同比增长分别为6.7%和5.3%，代入同比增长公式的变形式，就可以求出2001年全省一次能源产量。
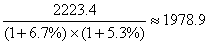万吨。
三、同比增长的“隐藏形式”
在资料分析题目中，有这样一种形式的同比增长，并不是以惯常所见的百分数形式给出，而是披上了一些“外衣”，需要考生看穿其本质。
【例题3】：2005年国家公务员考试一卷资料分析第三大题
1993－2003年某国国内生产总值指数
年份 | 国民生产总值 | 国内生产总值 | 第一产业 | 第二产业 | 第三产业 | 人均国内生产总值 |
1993 | 108.7 | 108.7 | 102.0 | 115.8 | 104.9 | 106.8 |
1994 | 98.4 | 98.4 | 98.2 | 97.5 | 100.4 | 96.9 |
1995 | 107.6 | 107.6 | 97.8 | 113.3 | 109.5 | 106.2 |
1996 | 111.7 | 111.7 | 104.1 | 115.0 | 113.7 | 110.2 |
1997 | 107.6 | 107.6 | 106.1 | 108.2 | 107.8 | 106.1 |
1998 | 107.8 | 107.8 | 98.5 | 113.6 | 105.9 | 106.5 |
1999 | 105.2 | 105.2 | 107.0 | 101.9 | 110.4 | 103.9 |
2000 | 109.3 | 109.1 | 111.5 | 105.6 | 113.0 | 107.5 |
2001 | 111.1 | 110.9 | 108.3 | 110.4 | 115.2 | 109.3 |
2002 | 115.3 | 115.2 | 112.9 | 114.5 | 119.4 | 113.7 |
2003 | 113.2 | 113.5 | 101.8 | 118.6 | 118.3 | 111.9 |
说明：本题中指数的计算方法为，当年的数值与上一年数值的比乘以100。举例来说，假设第一年的数值为m，第二年的数值为n，则第二年的指数为100×（n/m）
129.2003年与2001年相比，人均国内生产总值增长了（ ）
A.25.6％ B.27.2％ C.6.5％ D.24.3％
【答案】：B。
【新东方名师贾柱保解析】：根据表格下面的说明，我们可以发现，如果把表格中所给的指数先除以100再减1的话，恰好就是每一年相比于之前一年的同比增长。即2003年人均国内生产总值同比增长11.9%，2002年同比增长13.7%，明确了这一点之后就可以顺利进行计算。设2003、2002、2001三年的人均国内生产总值分别为A、B、C，那么2003年相比于2001年的增长为：
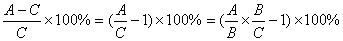
代入数值，可得（111.9%×113.7%—1）×100%=27.2%。
同比增长的计算是资料分析中一种基本的题目，也常常是考点设计所在，考生只要能够牢记同比增长的基本计算式与其变形，不难在短时间内列出计算式。但由于往往会涉及到除法和百分数的计算，因此对于考生的基本计算能力有较高的要求，能否又快又准地进行手算，才是同比增长计算题目真正的关键所在。
