专家分析各类公务员考试数字推理真题,结合常见的数字推理规律,总结出几条解决数字推理问题的优先法则:
1.数列项数很多,优先考虑组合数列。
2.数列出现特征数字,优先从特征数字入手。
3.数字增幅越来越大,优先从乘积、多次方角度考虑。
4.数列递增或递减,但幅度缓和,优先考虑相邻两项之差。
5.数列各项之间倍数关系明显,考虑作商或积数列及其变式。
6.分析题干数字的同时要结合选项中的数字,进一步判断数列规律。
要真正掌握数字推理难度很大,在下面的内容中,我们给出了数字推理的六大解题方法,并结合典型真题进行了解题分析,希望能给考生以最大的帮助。
一、从相邻项之差入手
考虑数列相邻项之差是解决数字推理问题的第一思维,在各类公务员考试数字推理题中等差数列及其变式出现的频率很大,也是必考题型,通过对数列相邻两项依次求差,得到新的数列,然后分析这个新数列的规律,可以直接或间接地得到原数列的规律。
等差数列及其变式所涉及的题型主要有二级等差数列及其变式和三级等差数列及其变式,很多情况下(三级等差数列及其变式)需要连续做差才能发现其中的规律。
特别注意的是,当所缺项位于数列中间时,由于从题干入手不能持续求差,这些题往往表现出一定的难度,此时需要假设其中的规律,然后通过做差加以验证。
例题:
1.5,5,5,12,5, ( )
A.3 B.1
C.24 D.26
解题分析:此题的题干数字对解题的提示作用不大,思路不明的时候还是从相邻两项之差入手,相邻两项之差依次是3.5,0,7,-7,这几个数的特征和规律也是很不明显,再次做差得到-3.5,7,-14,可以看出是公比为-2的等比数列,此题便得到了解决。

等差数列的变式情况很多,上题即是一个三级等差数列变式,由于第三级数列是一个正负交替的等比数列,所以题干数字并没有表现出明显的递增和递减趋势,这一类题难度较大。
在思路不明的情况下,分析相邻两项之差是很重要的方法。
二、分析相邻项之间的商、和、积
当题干数列某两项(或三项)的和、积、商关系明显时,可以优先考虑这种方法,此时从局部分析数列的能力显得尤为重要。考虑数列相邻项之和的方式主要有相邻两项之和与相邻三项之和。当数列数字有明显上升趋势,可以考虑相邻项之和或积;当数列相邻项之间存在明显的比例关系时,可以考虑相邻项的商。
例题:
2/3, 3, 4,14,58, ( )
A.814 B.836
C.802 D.828
解题分析:先看题干和选项,数字由14、58,变化到800多,这种信号暗示我们要从相邻项的乘积考虑,再看数列第一项为分数,与第二项3的乘积刚好为整数,这更确定了思路是正确的,简单比较发现,第一项与第二项求积,再加2得到了第三项,通过后面几项得到了验证,14×58=812,812+2=814,答案为A。
三、猜证数列各项之间的运算关系
数字推理规律种类繁多,其中一个大的类型就是数列各项在横向上存在相同或连续性的四则运算关系。
比较常见的类型有两种,一是前一项经过运算得到后一项,二是前面两项经过运算得到第三项。解这类题,往往通过对某几项(例如前两项或前三项)的分析,假设其中的规律,然后通过其他项加以验证,这中间可能有不断尝试的过程,一般从小数字入手。
最为常见有以下几种:
⑴ 前一项的倍数加常数或基本数列得到下一项;
⑵第一项的倍数加第二项的倍数得到第三项;
⑶前一项加上后一项简单运算后的结果得到第三项。
例题:
2, 5, 17, 71, ( )
A.149 B.359
C.273 D.463
解题分析:此题题干数字递增,再结合选项来看,涉及到倍数的可能较大,于是大致确定数字推理规律应是数列各项之间的运算关系。优先考虑前项运算得到后项的方式,先分析由第一项2到第二项5,可以是2的2倍加1、2的平方加1、2的3倍减1……,这时应想到一是倍数可能按规律变化,二是常数可能规律变化,结合第二项的5运算至17的方式(5的3倍加2、5的4倍减3……),最后确定了此题的规律。
2×2+1=5,5×3+1=17,17×4+3=71,71×5+4={359},其中乘数2、3、4、5和加数1、2、3、4都是连续自然数。
熟悉数字之间的运算关系对于解决数字推理问题十分重要,形成了一定的数字敏感度之后,解这类题就是一种直觉,平时应多加练习。
四、考虑数列各项的通项
在公务员考试数字推理题中,经常出现这样一类数列,数列各项可以用相类似的形式表示出来,如数列各项均可写成自然数的平方加1、数列各项均可写成连续自然数与连续质数的乘积……这一解题思路和基本数列类型中的多次方数列及其变式和整数乘积拆分数列相对应。例:
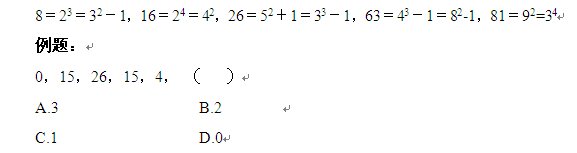

五、注意结构和位置
数字推理题中广泛出现了组合数列,包括间隔组合数列和分组组合数列两大类,这类题难度不大,关键在于通过对数列整体上的考察,发现其结构上的特点。
在解决图形形式数字推理时,考虑图形的结构和图形中数字的位置就更加重要。
例题:
2,3,6,9,14,15,30, ( )
A.21 B.37
C.35 D.24
解题分析:此题项数较多,间隔组合数列应优先考虑,奇数项依次是2、6、14、30,相邻两项依次做差得4、8、16,是公比为2的等比数列,于是认为奇数项是二级等差数列变式,这就肯定了此题是间隔组合数列的想法,再看偶数项,依次是3、9、15、( ),由前三项可假设是一个公差为6的等差数列,则应填入21,答案为A。
六、探求数列的整体特征
近年来数字推理求新求异,出现了许多创新形式的数字推理规律,这其中有很大一部分是考察数列各项的共有特征。数列各项表现出的共有特征主要存在于以下几个方面:整除性、质合性、排列顺序、数位组合运算、各位数字之和……。
例题:
422,352,516, 743,682, ( )
A.628 B.576
C.495 D.729
解题分析:数列各项都为三位数,数字增减不定,分析发现数字推理规律只能是各类创新形式数字推理规律之一。此题考察了数列各位数字之和,各项各位数字之和依次是8、10、12、14、16,因此所缺数字的各位数字之和应是18,即构成公差为2的等差数列。检查选项,发现B、C、D两项都符合这一特征,此时必须再加以分析,观察发现,数列每一项都有一个数字等于其他数字之和,第一项:4=2+2,第二项:5=3+2,第三项:6=5+1,第四项:7=4+3,第五项8=6+2,并且可以看出这个较大的数字在百位、十位、个位循环出现,因此最后一项这个较大数字应出现在个位,这样答案就唯一确定了,选D。