随着2014年考研日期的日趋临近,莘莘学子们正忙碌而紧张地进行着各考试科目的最后总复习,在各门考试科目中,数学作为一门公共科目,常常令一些考生感到头疼、没有把握,这一方面是因为数学本身的逻辑性、连贯性很强、公式多、计算量大,要学好它有一定难度,另一方面是因为某些考生以前对数学的重视程度不够,基础知识学得不够扎实,所以面对即将到来的大考信心不足。为了帮助这些考生能顺利通过考试,老师针对历年考研数学的题型特点,进行深入解剖,分析提炼出各种常考重要题型及方法,供考生们参考。下面主要分析数学三概率统计部分随机变量的数字特征的一类重要题型及解题方法。
题型:计算一维随机变量的数学期望和方差
计算一维随机变量的数学期望和方差是一个基本考点,常用的方法包括:
1)熟记6个重要的一维分布分布律和概率密度,及其数学期望和方差公式,这6个分布包括:0—1分布,二项分布,泊松分布,正态分布,均匀分布,指数分布;
2)熟练运用期望和方差的基本性质;
3)对应用题型要准确地理解题意并将应用问题正确地运用数学代数式表达出来。
例1.设随机变量X服从参数为1的泊松分布,则P{X=E(X2)}=________
分析:此题首先要求记得泊松分布的数学期望和方差,然后根据其分布律计算概率。 (2008年考研数学三真题第14题)
解:因为X服从参数为1的泊松分布,所以E(X)=D(X)=λ=1,由D(X)=E(X2)-[E(X)]2得E(X2)=D(X)+[E(X)]2=2,而P{X=k}=
,故P{X=E(X2)}=P{X=2)}=
例2.设随机变量X服从标准正态分布X~N(0,1),则E(Xe2X)}=________ (2013年考研数学三真题第14题)
分析:正态分布是最重要的分布,是每年考研必考点,对其概率密度和性质要熟记于胸,对其函数的期望的计算要熟练。
解:标准正态分布的概率密度为
,
例3.假设一设备开机后无故障工作的时间X服从指数分布,平均无故障工作的时间(EX)为5小时,设备定时开机,出现故障时自动关机,而在无故障的情况下工作2小时便关机,试求该设备每次开机无故障工作的时间Y的分布函数F(y). (2002年考研数学三真题第十二题)
分析:此题首先要将Y与X的相互关系表示出来,然后根据指数分布的性质进行计算。
解:由题意知X~E(λ),E(X)=1/λ=5,故λ=1/5,Y与X的关系:Y=min{X,2}
当y<0时,F(y)=P{Y≤y}=0
当y≥2时,F(y)=P{Y≤y}=1
当0≤y<2时,F(y)=P{Y≤y}=P{min{X,2}≤y}=P{X≤y}=
故Y的分布函数
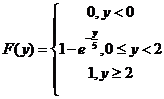
上面就是考研数学三概率统计部分随机变量的数字特征的一类重要题型及解题方法,以及应注意的事项,供考生们参考借鉴。在以后的时间里,老师还会陆续向考生们介绍其它常考重要题型及解题方法,希望各位考生留意查看。最后预祝各位考生在2014考研中取得佳绩。
推荐阅读:
读书人网为您最新整理研究生考试信息,敬请查阅,预祝各位考生顺利通过!