我这样战胜一道数学难题
初中数学,万变不离其宗,一切都建立在定义之上。总是坐享其成的我们,却没有料到老师今天突然破天荒地让我们去证明一个特别重要的定理——直角三角形斜边上的中线等于斜边的一半,而且还必须要用两种方法去证明,这真可是折煞我等!
刚刚学习了矩形,对于这一点我自然是不在话下。脑子里飞速的运转了解数学难题三步,即:
1. 分析已知求证
2. 画图写已知求证
3. 证明
看着这个直角三角形,我突然想起了听众享老师讲的倍长中线去证明全等三角形。于是我突发奇想:能不能使用倍长中线,将直角三角形扩充为矩形呢?说做就做,甚至连想都没有,环环相扣,很快就写写出了答案,令同学们目瞪口呆。
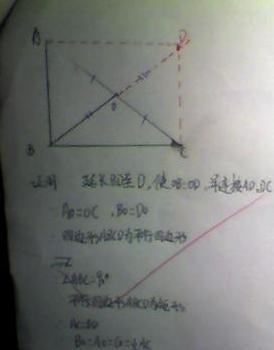
证明:延长BO至D,使OB=OD,连接AD、DC
∵AO=OC,BO=OD
∴四边形ABCD为平行四边形
∵∠ABC=90度
∴平行四边形ABCD为矩形
∴AC=BD
∴BO=AO=CO=1/2AC
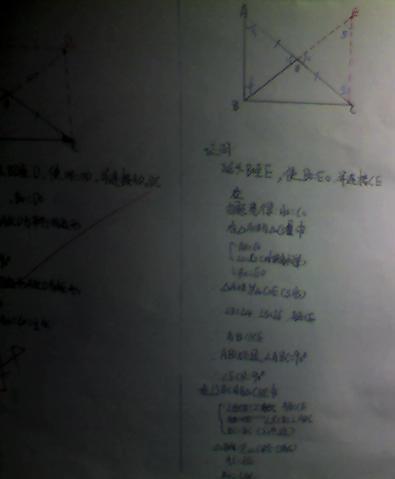
可是还需要用一个方法呢,我陷入了迷茫。矩形我已经用过了,难道我再去构造一个平行四边形吗?不,那和矩形大同小异。还是用勾股定理?可是我只知道一条边相等啊。于是我决定再“冒险”使用一次倍长中线,不过为了保险起见,顺便我连全等三角形的知识也牵扯进去。
一次又一次的试验,一次又一次的失败。不知失败了几十次,我总算第二次证明出来了。尽管花费了十几分钟,但是我竟然还是全班第一个证出来的。(证明过程在附图上)
这时,班里同学投来了敬佩的目光,我也满足了——这么多的心力没有白白花费。这节课虽然过去了,但是当想起“战胜难题”时,还总会不由自主的萦绕在心间……
附图:证明过程