圆跟矩形碰撞检测

圆和矩形碰撞检测

圆和矩形碰撞检测：

http://stackoverflow.com/questions/401847/circle-rectangle-collision-detection-intersection

Here is how I would do it:

bool intersects(CircleType circle, RectType rect){    circleDistance.x = abs(circle.x - rect.x);    circleDistance.y = abs(circle.y - rect.y);    if (circleDistance.x > (rect.width/2 + circle.r)) { return false; }    if (circleDistance.y > (rect.height/2 + circle.r)) { return false; }    if (circleDistance.x <= (rect.width/2)) { return true; }     if (circleDistance.y <= (rect.height/2)) { return true; }    cornerDistance_sq = (circleDistance.x - rect.width/2)^2 +                         (circleDistance.y - rect.height/2)^2;    return (cornerDistance_sq <= (circle.r^2));}

Here's how it works:

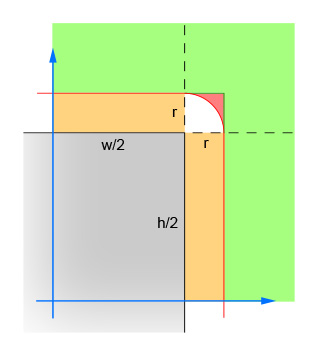
1. The first pair of lines calculate the absolute values of the x and y difference between the center of the circle and the center of the rectangle. This collapses the four quadrants down into one, so that the calculations do not have to be done four times. The image shows the area in which the center of the circle must now lie. Note that only the single quadrant is shown. The rectangle is the grey area, and the red border outlines the critical area which is exactly one radius away from the edges of the rectangle. The center of the circle has to be within this red border for the intersection to occur.

2. The second pair of lines eliminate the easy cases where the circle is far enough away from the rectangle (in either direction) that no intersection is possible. This corresponds to the green area in the image.

3. The third pair of lines handle the easy cases where the circle is close enough to the rectangle (in either direction) that an intersection is guaranteed. This corresponds to the orange and grey sections in the image. Note that this step must be done after step 2 for the logic to make sense.

4. The remaining lines calculate the difficult case where the circle may intersect the corner of the rectangle. To solve, compute the distance from the center of the circle and the corner, and then verify that the distance is not more than the radius of the circle. This calculation returns false for all circles whose center is within the red shaded area and returns true for all circles whose center is within the white shaded area.