【计算机图形学】3-1 二维几何变换基本理论
我们用齐次坐标来记录一个点的位置,如果自行推导就会发现,不用齐次坐标无法实现坐标平移的变换矩阵。坐标的变换由齐次坐标乘上一个矩阵实现,考虑二维情况,齐次坐标是一个1×3的向量,变换为3×3的矩阵,所以相乘之后还是一个齐次坐标。这样,多次变换的累加就相当于变换矩阵相乘,算好矩阵之后,所有坐标乘上最终的矩阵就是点最终的位置,这样可以省下大量的时间,不必对每一个点做所有的变换。
注:公式解释语言是LibreOffice中的。
leftlbrace binom{x' = x + Tx}{y' = y +Ty} right none
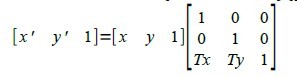
[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{1 # 0 # 0 ## 0 # 1 # 0## Tx # Ty # 1} right ]
复合平移变换:
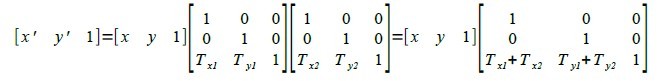
[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{1 # 0 # 0 ## 0 # 1 # 0## T_{x1} # T_{y1} # 1} right ]left [matrix{1 # 0 # 0 ## 0 # 1 # 0 ##T_{x2} # T_{y2} # 1} right ] = [matrix{x # y # 1}] left [matrix{1 # 0# 0 ## 0 # 1 # 0 ## T_{x1}+T_{x2} # T_{y1}+T_{y2} # 1} right ]
leftlbrace binom{x' = Sx cdot x}{y' = Sy cdot y} right none

[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{Sx # 0 # 0 ## 0 # Sy #0 ## 0 # 0 # 1} right ]
复合比例变换:

[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{S_{x1} # 0 # 0 ## 0 #S_{y1} # 0 ## 0 # 0 # 1} right ]left [matrix{S_{x1} # 0 # 0 ## 0 #S_{y1} # 0 ## 0 # 0 # 1} right ] =[matrix{x # y # 1}] left[matrix{S_{x1} cdot S_{x2} # 0 # 0 ## 0 # S_{y1} cdot S_{y2} # 0 ## 0# 0 # 1} right ]
如果想关于某点进行比例变换,可以先平移到这个点,进行比例变换,再平移回来。

matrix{{[matrix{x'# y' # 1}]} # alignl`=`{[matrix{x # y # 1}] left [matrix{1 # 0 # 0 ##0 # 1 # 0 ## -x_{0} # -y_{0} # 1} right]left [matrix{a # 0 # 0 ## 0 #d # 0 ## 0 # 0 # 1} right]left[matrix{1 # 0 # 0 ## 0 # 1 # 0 ## x_{0}# y_{0} # 1} right]} ## {} # {alignl`=`[matrix{x # y # 1}] left[matrix{1 # 0 # 0 ## 0 # 1 # 0 ## (1-a)cdot x_{0} # (1-d)cdot y_{0} #1} right ]}}
leftlbrace binom{x' = x cdot cosθ-y cdot sinθ}{y' = x cdot sinθ+y cdotcosθ} right none

[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{cosθ # sinθ # 0 ##-sinθ # cosθ # 0 ## 0 # 0 # 1} right ]
复合旋转变换:
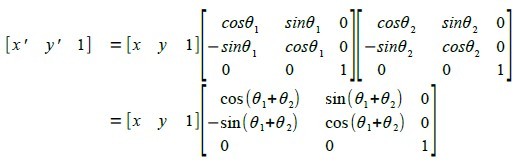
matrix{{[matrix{x'# y' # 1}]}#{alignl`=`[matrix{x # y # 1}] left [matrix{cosθ_{1} #sinθ_{1} # 0 ## -sinθ_{1} # cosθ_{1} # 0 ## 0 # 0 # 1} right ]left[matrix{cosθ_{2} # sinθ_{2} # 0 ## -sinθ_{2} # cosθ_{2} # 0 ## 0# 0 # 1} right ]}##{}#{alignl`=`[matrix{x # y # 1}] left[matrix{cos(θ_{1}+θ_{2}) # sin(θ_{1}+θ_{2}) # 0 ##-sin(θ_{1}+θ_{2}) # cos(θ_{1}+θ_{2}) # 0 ## 0 # 0 # 1} right ]}}
如果想关于某点进行旋转变换,可以先平移到这个点,进行旋转变换,再平移回来。
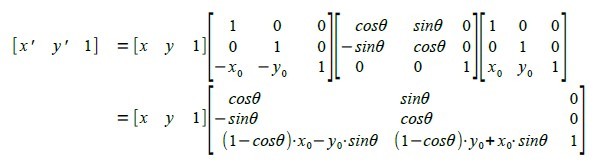
matrix{{[matrix{x'# y' # 1}]} # alignl`=`{[matrix{x # y # 1}] left [matrix{1 # 0 # 0 ##0 # 1 # 0 ## -x_{0} # -y_{0} # 1} right]left [matrix{cosθ # sinθ #0 ## -sinθ # cosθ # 0 ## 0 # 0 # 1} right ]left[matrix{1 # 0 # 0 ##0 # 1 # 0 ## x_{0} # y_{0} # 1} right]} ## {} # {alignl`=`[matrix{x #y # 1}] left [matrix{cosθ # sinθ # 0 ## -sinθ # cosθ # 0 ##{(1-cosθ)cdot x_{0} - y_{0} cdot sinθ} # {(1-cosθ)cdot y_{0} +x_{0} cdot sinθ} # 1} right ]}}
leftlbrace binom{alignl x' = x}{alignl y' = -y} right none

[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{1 # 0 # 0 ## 0 # -1 #0 ## 0 # 0 # 1} right ]
(2)关于y轴对称
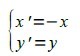
leftlbrace binom{alignl x' = -x}{alignl y' = y} right none
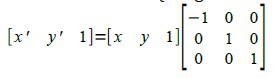
[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{-1 # 0 # 0 ## 0 # 1 #0 ## 0 # 0 # 1} right ]
(3)关于原点对称

leftlbrace binom{x' = -x}{y' = -y} right none
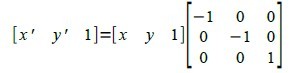
[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{-1 # 0 # 0 ## 0 # -1 #0 ## 0 # 0 # 1} right ]
leftlbrace binom{x' = x + by}{y' = dx + y} right none
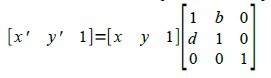
[matrix{x'# y' # 1}] = [matrix{x # y # 1}] left [matrix{1 # b # 0 ## d # 1 # 0## 0 # 0 # 1} right ]
leftlbrace binom{x_{v} - vxl = {vxr - vxl} over {wxr - wxl} (x_{w} -wxl)}{y_{v} - vyb = {vyt - vyb} over {wyt - wyb} (y_{w} - wyb)} rightnone
简化后的格式就是x= ax + b, y = cx + d,所以就是平移+比例变换的复合。