POJ 2187 Beauty Contest 结构凸包 + 旋转卡壳

POJ 2187 Beauty Contest 构造凸包 + 旋转卡壳

在刷了一整版的 TLE 和 WA 外加一个CE和几个OLE之后终于拿到了第一个旋转卡壳的AC。。。泪奔

http://blog.csdn.net/ACMaker/archive/2008/10/29/3176910.asp

http://cgm.cs.mcgill.ca/~orm/rotcal.frame.html

历史：

1978年， M.I. Shamos's Ph.D. 的论文"Computational Geometry"标志着计算机科学的这一领域的诞生。 当时他发表成果的是一个寻找凸多边形直径的一个非常简单的算法， 即根据多边形的一对点距离的最大值来确定。 
后来直径演化为由一对对踵点对来确定。 Shamos提出了一个简单的 O(n) 时间的算法来确定一个凸 n 角形的对踵点对。 因为他们最多只有 3n/2 对， 直径可以在 O(n) 时间内算出。 
如同Toussaint后来提出的， Shamos的算法就像绕着多边形旋转一对卡壳。 因此就有了术语“旋转卡壳”。 1983年， Toussaint发表了一篇论文， 其中用同样的技术来解决许多问题。 从此， 基于此模型的新算法就确立了， 解决了许多问题。 

他们包括： 

计算距离凸多边形直径凸多边形宽凸多边形间最大距离凸多边形间最小距离外接矩形最小面积外接矩形最小周长外接矩形三角剖分洋葱三角剖分螺旋三角剖分四边形剖分凸多边形属性合并凸包找共切线凸多边形交临界切线凸多边形矢量和最薄截面最薄横截带

凸多边形直径我们将一个多边形上任意两点间的距离的最大值定义为多边形的直径。 确定这个直径的点对数可能多于一对。 事实上， 对于拥有 n 个顶点的多边形， 就可能有 n 对“直径点对”存在。 

 

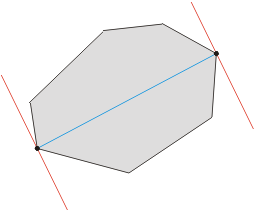
一个多边形直径的简单例子如左图所示。 直径点对在图中显示为被平行线穿过的黑点 （红色的一对平行线）. 直径用浅蓝色高亮显示。


显然， 确定一个凸多边形 P 直径的点对不可能在多边形 P 内部。 故搜索应该在边界上进行。 事实上， 由于直径是由多边形的平行切线的最远距离决定的， 所以我们只需要查询对踵点。 Shamos (1978) 提供了一个 O(n) 时间复杂度计算n点凸包对踵点对的算法。直径通过遍历顶点列表， 得到最大距离即可。 如下是1985年发表于 Preparata 和 Shamos 文章中的 Shamos 算法的伪代码。 
输入是一个多边形 P={p1,...,pn}. 



begin     p0:=pn;     q:=NEXT[p];     while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q)) do          q:=NEXT[q];          q0:=q;          while (q != p0) do               begin                    p:=NEXT[p];                    Print(p,q);                    while (Area(p,NEXT[p],NEXT[q]) > Area(p,NEXT[p],q) do                         begin                              q:=NEXT[q];                              if ((p,q) != (q0,p0)) then Print(p,q)                              else return                         end;                    if (Area(p,NEXT[p],NEXT[q]) = Area(p,NEXT[p],q)) then                      if ((p,q) != (q0,p0)) then Print(p,NEXT[q])                      else Print(NEXT[p],q)               endend.


此处 Print(p,q) 表示将 (p,q) 作为一个对踵点对输出， Area(p,q,r) 表示三角形 pqr 的有向面积。 
虽然直观上看这个过程与常规旋转卡壳算法不同， 但他们在本质上是相同的， 并且避免了所有角度的计算。 

如下是一个更直观的算法：

计算多边形 y 方向上的端点。 我们称之为 ymin 和 ymax 。通过 ymin 和 ymax 构造两条水平切线。 由于他们已经是一对对踵点， 计算他们之间的距离并维护为一个当前最大值。同时旋转两条线直到其中一条与多边形的一条边重合。一个新的对踵点对此时产生。 计算新的距离， 并和当前最大值比较， 大于当前最大值则更新。重复步骤3和步骤4的过程直到再次产生对踵点对 (ymin,ymax) 。输出确定最大直径的对踵点对。

至此， 上述的过程（伪代码中的）显得十分有用， 我们可以从对踵点对中得到其他的信息， 如多边形的宽度 。




#include <iostream>#include <cstring>#include <cstdlib>#include <cstdio>#include <queue>#include <cmath>#include <algorithm>using namespace std;struct P{    double x,y,a;}p[50010],s[50010],re;double calangle(P a,P b){    if(a.x == b.x && a.y == b.y)        return -2;    return  acos( (b.x-a.x)/(2*sqrt((b.x-a.x)*(b.x-a.x) + (b.y-a.y)*(b.y-a.y) )) );}double calangle(P v1,P a,P b){    P v2;    v2.x = b.x-a.x;    v2.y = b.y-a.y;    return acos( (v1.x*v2.x + v1.y*v2.y)/(2*sqrt((v1.x*v1.x + v1.y*v1.y)*(v2.x*v2.x + v2.y*v2.y))) );}bool cmp(P p1,P p2){    if(p1.a < p2.a)        return true;    if(p1.a == p2.a && p1.y < p2.y)        return true;    if(p1.a == p2.a && p1.y == p2.y && p1.x < p2.x)        return true;    return false;}bool judgesite(P p1,P p2,P p3){    P t1,t2;    t2.x = p2.x-p1.x;    t2.y = p2.y-p1.y;    t1.x = p3.x-p1.x;    t1.y = p3.y-p1.y;    if(t2.x*t1.y - t1.x*t2.y > 0)//此处 >= 0 将会添加共线点        return true;    return false;}int top;double CalMaxDiameter(P *p,int n){    // p 为凸包上点 逆时针排列    // n 为数量    P p1,p2;//两个对踵点    P v1 = {0,-1,0},v2 = {0,1,0};//两个射线    int s1,s2;//两个对重点的坐标    int n1,n2;    double a1,a2;    double MaxDiameter = -1,TempDiameter;//记录最大直径    p1.x =  1000000;    p2.x = -1000000;    //寻找第一对对踵点 最左边的 和 最右边的肯定是一对对踵点    for(int i = 0;i < n; ++i)    {        if(p[i].x > p2.x || (p[i].x == p2.x && p[i].y > p2.y))        {            s2 = i;            p2 = p[i];        }        if(p[i].x < p1.x || (p[i].x == p1.x && p[i].y < p1.y))        {            s1 = i;            p1 = p[i];        }    }    MaxDiameter = (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);    n1 = s1;    n2 = s2;    while( (n1 != s2 || n2 != s1))    {        a1 = calangle(v1,p[n1],p[(n1+1)%n]);        a2 = calangle(v2,p[n2],p[(n2+1)%n]);        if(a1 < a2)        {            v1.x = p[(n1+1)%n].x - p[n1].x;            v1.y = p[(n1+1)%n].y - p[n1].y;            v2.x = -v1.x;            v2.y = -v1.y;            n1 = (n1+1)%n;        }        else        {            v2.x = p[(n2+1)%n].x - p[n2].x;            v2.y = p[(n2+1)%n].y - p[n2].y;            v1.x = -v2.x;            v1.y = -v2.y;            n2 = (n2+1)%n;        }        TempDiameter = (p[n1].x - p[n2].x)*(p[n1].x - p[n2].x) + (p[n1].y - p[n2].y)*(p[n1].y - p[n2].y);        if(MaxDiameter < TempDiameter)                MaxDiameter = TempDiameter;    }    return MaxDiameter;}int main(){    int n;    int i;    while(scanf("%d",&n) != EOF)    {        for(i = 0;i < n; ++i)        {            scanf("%lf %lf",&p[i].x,&p[i].y);        }        //寻找参考点        for(re = p[0],i = 1; i < n; ++i)        {            if(re.y > p[i].y || (re.y == p[i].y && re.x > p[i].x))                re = p[i];        }        //计算p[i] 与 参考点 与 x轴正方向形成的夹角        for(i = 0;i < n; ++i)        {            p[i].a = calangle(re,p[i]);        }        sort(p,p+n,cmp);        //去重点        top = 0;        for(s[top++] = p[0],i = 1;i < n; ++i)        {            if(p[i].x != p[i-1].x || p[i].y != p[i-1].y)                s[top++] = p[i];        }        for(i = 0;i < top; ++i)        {            p[i] = s[i];        }        n = top;        top = 0;        s[top++] = p[0];        s[top++] = p[1];        for(i = 2;i < n;)        {            if(top < 2 || judgesite(s[top-2],s[top-1],p[i]))            {                s[top++] = p[i];                ++i;            }            else top--;        }        printf("%d\n",(int)CalMaxDiameter(s,top));    }    return 0;}