图像处理特征不变算子系列之SUSAN算子(三)
kezunhai@gmail.com
http://blog.csdn.net/kezunhai
在前面分别介绍了:图像处理特征不变算子系列之Moravec算子(一)和图像处理特征不变算子系列之Harris算子(二)。今天我们将介绍另外一个特征检测算子---SUSAN算子。SUSAN算子很好听的一个名字,其实SUSAN算子除了名字好听外,她还很实用,而且也好用,SUSAN的全名是: Smallest Univalue Segment Assimilating Nucleus,关于这个名词的翻译国内杂乱无章,如最小核值相似区、最小同值收缩核区和最小核心值相似区域等等,个人感觉这些翻译太过牵强,我们后面还是直接叫SUSAN,这样感觉亲切,而且上口。
SUSAN算子是一种高效的边缘和角点检测算子,并且具有结构保留的降噪功能(structure preserving noise reduction )。那么SUSAN是什么牛气冲天的神器呢?不仅具有边缘检测、角点检测,还具备结构保留的降噪功能。下面就让我娓娓地为你道来。
1)SUSAN算子原理
为了介绍和分析的需要,我们首先来看下面这个图:

该图是在一个白色的背景上,有一个深度颜色的区域(dark area),用一个圆形模板在图像上移动,若模板内的像素灰度与模板中心的像素(被称为核Nucleus)灰度值小于一定的阈值,则认为该点与核Nucleus具有相同的灰度,满足该条件的像素组成的区域就称为USAN(Univalue Segment Assimilating Nucleus)。
接下来,我们来分析下上图中的五个圆形模的USAN值。对于上图中的e圆形模板,它完全处于白色的背景中,根据前面对USAN的定义,该模板处的USAN值是最大的;随着模板c和d的移动,USAN值逐渐减少;当圆形模板移动到b处时,其中心位于边缘直线上,此时其USAN值逐渐减少为最大值的一半;而圆形模板运行到角点处a时,此时的USAN值最小。因此通过上面的描述:我们可以推导出:边缘处的点的USAN值小于或等于最大值一半。由此,我们可以得出SUSAN提取边缘和角点算法的基本原理:在边缘或角点处的USAN值最小,可以根据USAN区域的大小来检测边缘、角点等特征的位置和方向信息。
上面都是口头阐述,文字的力量是单薄的,下面我们进入公式阶段。SUSAN算子通过用一个圆形模板在图像上移动,一般这个圆形模板的半径是(3.4pixels)的包含37个像素。模板内的每一个像素与中心像素进行比较,比较方式如下所示:
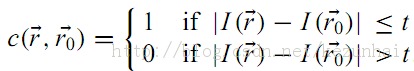
其中是中心像素,
是掩膜内的其他像素,t是一个像素差异阈值(通常对于对比度比较低的区域,选取较小的t;反之,则t的阈值可以选择大些)。 接着,对上式进行统计,统计方式如下式:
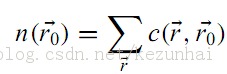
得到的n值就是USAN的大小。
得到USAN值后,通过阈值化就可以得到初步的边缘响应,公式表示如下:
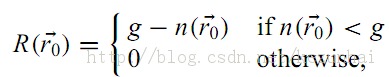
其中,g=![]() ,也即g的取值为USAN最大值的3/4。USAN值越小,边缘的响应就越强。
,也即g的取值为USAN最大值的3/4。USAN值越小,边缘的响应就越强。
得了出事的边缘响应进行非极大值抑制,就可以得到图像的边缘信息了。上张SUSAN边缘检测的效果图:

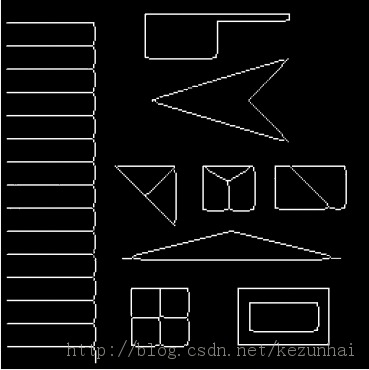
以上完成了SUSAN检测边缘的功能,或许你已经想到了怎么用SUSAN算子来检测角点了。通过上面对a、b、c、d、e等几个圆形模板的USAN值的分析,当模板的中心位于角点处时,USAN的值最小。下面简单叙述下利用SUSAN算子检测角点的步骤:
1)利用圆形模板遍历图像,计算每点处的USAN值
2)设置一阈值g,一般取值为1/2(Max(n), 也即取值为USAN最大值的一半,进行阈值化,得到角点响应
3)使用非极大值抑制来寻找角点。
通过上面的方式得到的角点,存在很大伪角点。为了去除伪角点,SUSAN算子可以由以下方法实现:①计算USAN区域的重心,然后计算重心和模板中心的距离,如果距离较小则不是正确的角点;②判断USAN区域的重心和模板中心的连线所经过的像素都是否属于USAN区域的像素,如果属于那么这个模板中心的点就是角点。
总结:SUSAN算子是一个原理简单、易于了解的算子。由于其指数基于对周边象素的 灰度比较,完全不涉及梯度的运算,因此其抗噪声能力很强,运算量也比较小;同时,SUSAN算子还是一个各向同性的算子;最后,通过控制参数t和g,可以根据具体情况很容易地对不同对比度、不同形状的图像通过设置恰当的t和g进行控制。比如图像的对比度较大,则可选取较大的t值,而图像的对比度较小,则可选取较小的t值。总之,SUSAN算子是一个非常难得的算子,不仅具有很好的边缘检测性能;而且对角点检测也具有很好的效果。
更多信息请参考:
1、SUSAN Low Level Image Processing:http://users.fmrib.ox.ac.uk/~steve/susan/
2、OpenCV的susan角点检测:http://blog.csdn.net/augusdi/article/details/9012555
作者:kezunhai 出处:http://blog.csdn.net/kezunhai 欢迎转载或分享,但请务必声明文章出处。