【课程论文】一种基于消失点的单幅未校图像测量新方法
一种基于消失点的单幅未校图像测量新方法
摘 要:针对从未知拍摄参数的单个图像或视频中推知目标物的三维信息的需要,人们进行了大量研究,但多数是围绕如何较好地估计出图像至地面的单应性矩阵,并且可测范围比较局限。本文提出利用三个消失点和一个参考高度,对基于小孔成像几何关系的测量模型中所需参数进行估计,进而完成测量。该方法相对于先前的单目测量方法,因为没有矢量和矩阵运算而显简洁高效,并且大大扩展了可测范围,更能适用于视频分析中。实验结果表明,本文所提模型及参数估计方法有效、可行。
关键字:单目测量;消失点;金字塔模型;参数估计
A Novel Approach for Single Uncalibrated Image Based Vanishing Points
Abstract: In order to deduce the 3D information of the targets from a single image or video without the camera parameters, people had undertaken extensive research,
but most focu on how to better estimate the homography of the image to the ground, and the detection range is more limited. This paper presents a novel approach to
solve it with the measurement model under pinhole imaging geometry, and the parameters of the model are estimated by three vaishing points and a reference height.
And then we can complete the measurement easily. Compared to the previous, this method is more simple and efficient because of without vector and matrix operations,
and greatly expandes the range of measurable, more suitable for video analysis. Experimental results show that the proposed model and parameter estimation method
is effective and feasible.
Key words: Single View Metrology;Vanishing Points;Pyramid Model;Parameter Estimation
0 引 言视觉测量技术,是指“依据某些已知条件,试图从物体的二维图像中估计出其三维几何尺寸”;相对于其它传感器技术,具有非接触、结构简单、数据采集迅速、应用广泛等优点而受到人们的长期关注和研究,而从一幅由未知摄像机参数拍摄的图像中推知三维信息的单目测量技术则更是受到人们的追捧[1~7]。
一种经典的单目测量方法[1]:通过参考平面上两对点来确定参考平面的消失线,然后再根据不平行于参考平面的参考方向的消失点和参考高度,估计出透视矩阵,再结合交比,就可以测量指定方向上的高度、平行于参考平面的平面上的目标面积或长度的比率以及推算摄像机位置。在此基础上,将两对点变更为两组平行线,一定程度上可提高计算消失点的稳定性[2]。Jie Shao等人[3]则将单目测量方法应用于视频,通过跟踪运动目标来确定消失点。此类方法局限是必须要能从图像中找出三个消失点,且不能测量参考平面上的点。
文献[4]利用参考平面上的消失线及两个不平行的线段长度,文献[5]则利用两个平行圆以及其中之一的直径,实现了参考平面上或平行面上点的测量,但对于视见空间内的点的高度仍无法测定。
文献[6]利用两个或者三个相互垂直的消失点以及一个参考长度,估计出透视矩阵,然后用其线性的办法估计出消失点正交所构成的平面上的两点距离,相对地扩大
了测量范围,但还是不测量平面外的点。
文献[7]利用三个消失点和一个参考高度,较完整的估计出透视矩阵,实现了对参考平面内两点距离及空间点高度的测量,其局限是不能测量平行于参考平面上的两点距离。
而文献[8][9]所提出的单目测量模型,简单方便,理论上可以实现对整个视见空间的测量,并且该测量模型适应于视场中没有消失点或只有两个消失点的特殊情形。本文对此测量模型进行了应用扩展,并针对视场中存在三个消失点的一般情形,提出基于三个消失点和一个参考高度的空间几何约束关系,对单目测量模型中所需参数进行估计,然后方便地测量参考平面上任意两点距离、空间点到参考平面的高度以及平行于参考平面的平面上的任意两点距离。
1 金字塔测量模型[8][9]
在很多视觉测量应用场景中,都是以摄像机为中心主体来感知外界,而它的视见空间是一个以光心Oc为顶点、沿光轴OcZc负向展开的金字塔空间,如图1所示。
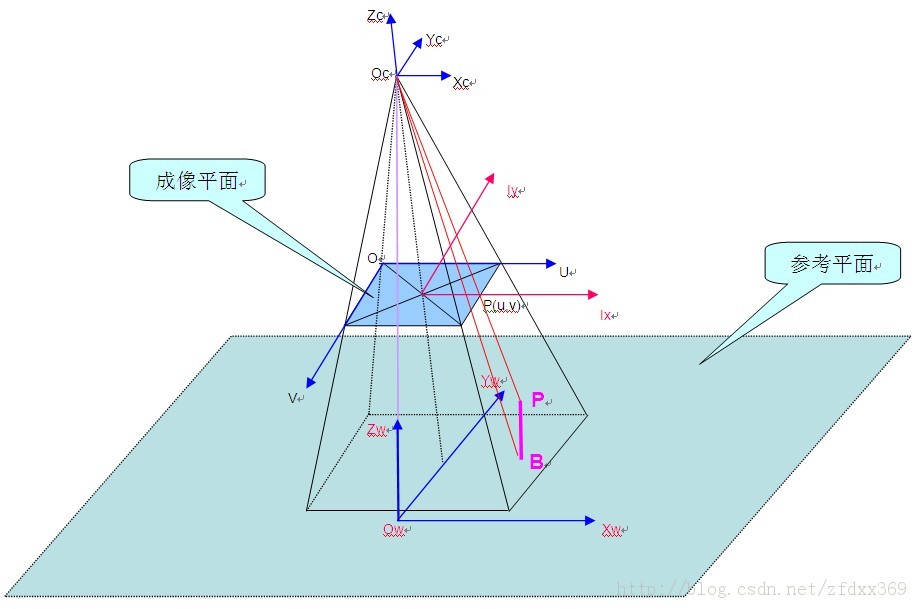
图1 金字塔单目测量模型
Fig.1 Pyramid measurement model
以摄像机光心在参考平面上的投影点作为世界坐标系的原点,如图1所示建立起相应的坐标系统:OwXwYwZw为世界坐标系,主要用于描述空间目标实体三维信息;OcXcYcZc为摄像机坐标系,主要用于描述摄像机相对于世界坐标系的位置状态;OUV为计算机图像坐标系,主要用于描述空间目标实体在成像平面上的位置信息;OIxIy为图像主点坐标系,主要用于描述空间目标实体的成像位置偏离图像主点的情况。
世界坐标系与摄像机坐标系的关系:点Ow是Oc在参考平面上的投影点;OwXw轴与OcXc轴平行且正向相同,具体方向取自参考平面上无限远点在成像平面上的消失线;OwYw轴、OwZw轴与OcYc轴共面;其中OwYw轴与OcZc轴夹角我们定义为摄像机俯仰角θ。
计算机图像坐标系与图像主点坐标系的关系:设光心在成像平面的投影坐标为 (uo ,vo),则它们的关系如式(1)所示:
 (1)
(1)
计算机图像坐标系与摄像机坐标系的关系: OcZc轴(即光轴)垂直于成像平面;OcXc轴平行于成像平面上的水平消失线;其中OU轴与水平消失线之夹角我们定义为摄像机侧倾角φ,应用时我们需要首先按式(2)进行修正,保证OU轴与OcZc轴平行。
 (2)
(2)
设记点Oc至点Ow的距离为H,摄像机焦距f,像素单元物理尺寸dx、dy,则逻辑焦距fx=dx/f、fy=dy/f,对于视见空间里任意一点P(PXw ,PYw ,PZw)及其在OwXwYw平面(参考平面)上的投影点B(PXw ,PYw ,0),在成像平面上的图像主点坐标分别P’(Px,Py) 和B’(Bx,By)[已经式(2)修正],则由图2中所描述的光学几何关系有:
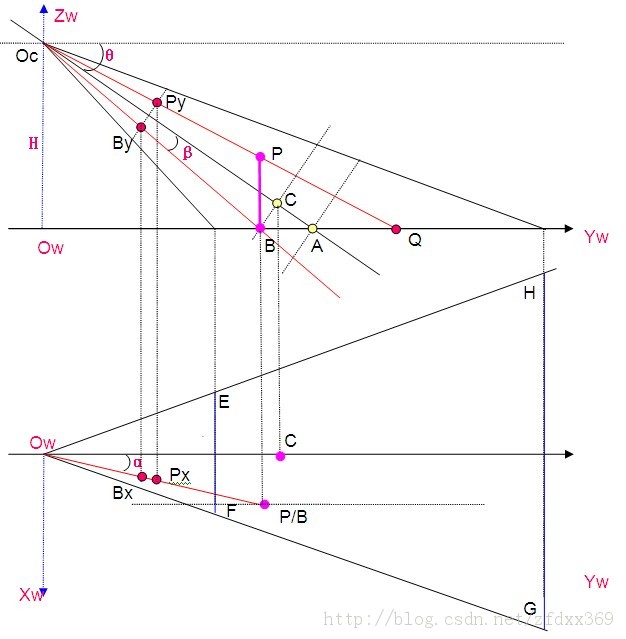
图2 金字塔测量模型的侧视图和俯视图(侧倾角φ=0)
Fig.2 side view and top view of the Pyramid measurement model
 (3)
(3)
其中,
整理可得:
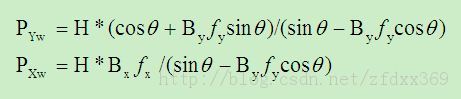 (4)
(4)
由于P、Q两点共线,因此对于PZw按式(5)给出:
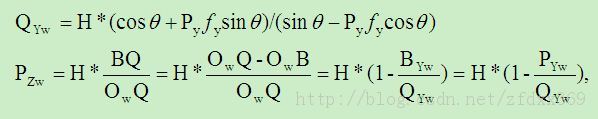 (5)
(5)
对于俯仰角θ=0的特殊情形,空间点P的世界坐标按(6)给出:
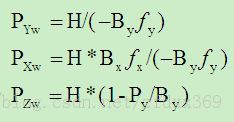 (6)
(6)
对于俯仰角θ=90度的特殊情形,可由式(4)直接给出,只需要估计出像素单元物理尺寸dx、dy,就可以测量参考平面上任意两点距离,而对于平行于参考平面的高度测量则需要另行给定一个待测平面上参考长度量,此时对于该平面上的任意两点距离也是可实现测量的。
由于视场中没有消失点或者只有两个消失点的特殊情形,在一般的图像处理中比较少出现,加之处理也比较简单,所以本文专注于讨论视场中存在三个消失点的情形。
从前文的阐述中易知,金字塔单目测量模型中所需要的参数有:图像主点坐标(u0,v0)、摄像机侧倾角φ、摄像机俯仰角θ、摄像机光心高度H以及摄像机逻辑焦距fx和fy,因些在接下来的第3节将会介绍如何利用三个消失点和一个参考高度的空间几何约束关系,估计出这些参数值。
2 模型参数估计方法
首先,较为符合实际情况地假定摄像机像素两个方向的物理尺寸大小相等dx=dy,进而相应的逻辑焦距也就相等,即fx=fy。
提取参考平面上两组相互垂直的平行线和一组垂直参考平面的平行线在成像平面上的交点,也就是消失点,记为V1、V2和V3,相应的计算机图像坐标为(V1u , V1v)、(V2u , V2v)和(V3u , V3v)。此时,我们可以得出如图3所示的三个消失点与光心及焦距之间的几何关系:点Oc为摄像机光心;面OcV1V2平行于参考平面,且角V1OcV2为直角;面V1V2V3为成像平面;线段OcN垂直面V1V2V3,其长度值就是摄像机的焦距;线V3Oc垂直面OcV1V2;角MOcN就是摄像机的倾斜角θ。过点V3对线V1V2作垂线V3M于垂足M(Mu,Mv)。
图3 三个消失点与光心的位置关系示意图
Fig.3 the geometric relationship among the three vanishing points and the optical center
2.1 俯仰角θ估计因线V1V2同时垂直线OcV3和线OcN,故线V1V2垂直面OcV3M,进而线V1V2垂直线OcM和线V3M,从而可得式(7):
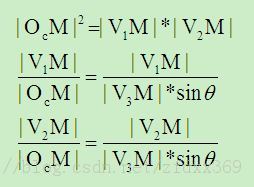 (7)
(7)
可解得摄像机的倾斜角θ满足式(8),一般地,倾斜角θ正负取同sign(V3v –Mv):
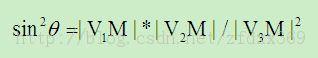 (8)
(8)
摄像机的逻辑焦距按式(9)导出:
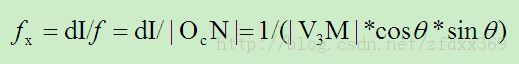 (9)
(9)
摄像机主点位置(u0,v0)按式(10)给出:
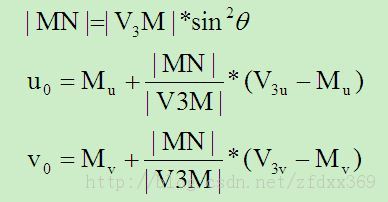 (10)
(10)
侧倾角φ的估计可由式(11)给出:
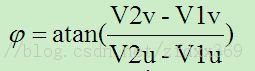 (11)
(11)
对于摄像机光心高度H的估计,可以利用参考高度结合交比估计出来,但在这里我们可以方便地利用前面已经得出的参数,假定光心高度为一个单位即H1=1,结合式(1)(2)(4)(5),可以算得参考高度h的值为h1,那么由式(5)-2易知摄像机光心高度H如式(12)所示:
H=h/h1 (12)
由此可见,能否对消失点进行正确的估计,直接影响到上述参数估计的准确性,文献 [10~13]提出了一系列消失点估计算法均可借鉴。
基于消失点的单目空间坐标测量算法流程如下:
A,确定三个消失点;
B,估计测量模型参数;
C,依次按式(1)(2)(4)(5)进行计算;
D,按欧氏距离计算两点距离。
如果是在视频流中对运动目标进行持续跟踪测量,则可以事先一次性地对每一像素计算出Xw和Yw,形成两张距离表,Zw按式(5)动态算出,这样就可以大大提高测量系统的实时性。如果需要测量平行于参考平面的平面上的点,只需要相应地调整摄像机光心高度H值。
3 对比实验
为了检验本文所述方法的有效性,同时为了方便比较,测量所用图片为文献[7]中的一张典型图片[14],三个消失点也是类似地在图片中选择三组两条平行线上的点,拟合成直线算得交点:V1(-909.45,-427.97)、V2(1331.60,-455.33)、V3(388.16,1372.60)。

图4 三个消失点估计所用平行线组及参考高度
Fig.4 the three groups of parallel lines and the reference height

图5 测量位置
Fig.5 the measured positions
表1高度测量结果对比
Table 1 comparison of the measurement results of height
(单位:cm) H1 H2 H3 H4 H5 H6
真实值 97.0 97.0 97.0 --- --- ---
文献[7] 96.9 97.1 97.2 180.1 174.9 175.6
本 文 96.7 97.3 98.1 184.5 176.9 176.1
表2长度测量结果对比
Table 2 comparison of the measurement results of length
(单位:cm)L1 L2 L3 L4 L5 L6 L7 L8
真实值 180.0 180.0 180.0 180.0 180.0 180.0 180.0 180.0
文献[7] 188.0 194.4 188.3 194.8 188.0 195.4 189.5 195.8
本 文 175.4 173.1 174.0 170.7 174.8 175.1 174.8 173.6
从表1和表2的具体数据比对当中可以看出,测量结果之差异相对于测量目标来说还是可以接受的,基本上验证了本文所提出的参数估计方法用于金字塔测量模型是切实可行的,并且,算法上也因为没有矢量和矩阵运算而相对地要简洁明了许多。
4 结 论
本文针对金字塔测量模型提出的参数估计方法,简单方便实用,但是对消失点及参考高度比较敏感。由于测量模型中没有考虑摄像机的非线性畸变,所以多适用于测量精度要求不很高的场合,但是,如果先使用文献[15][16]的方法来标定摄像机内部参数,再用本文的方法来标定摄像机外部参数,则可以获得较好的测量精度。
另外,对于视见空间中任意一点,较快捷准确地找出其在参考平面或平行面上的投影点,则是需要更进一步地研究。
[1] A Criminisi, I D Reid, and A Zisserman. Single View Metrology[R]. In Proc. Int. Conf. Computer Vision, pages 434–441, 1999.
[2]G H Wang,Z Y Hu and F C Wu,Single view based measurement on space planes[J],Journal of Computer Science and Technology,Vol.19(3),2004.
[3] Jie Shao, Shaohua Kevin Zhou, Rama Chellappa.Robust Height Estimation of Moving Objects From Uncalibrated Videos[J]. IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 19, NO. 8, AUGUST 2010.
[4] Guanghui Wang; Yihong Wu,Zhanyi Hu.A Novel Approach for Single View Based Plane Metrology[R]. Pattern Recognition, 2002. Proceedings. 16th International Conference on. Page(s): 556 - 559 vol.2.
[5] Nan Jiang and Zhongding Jiang.DISTANCE MEASUREMENT FROM SINGLE IMAGE BASED ON CIRCLES[R]. Acoustics, Speech and Signal Processing, 2007. IEEE International Conference on . Page(s): I-809-812.
[6] Kun Peng,Lulu Hou, Ren Ren,etc.Single View Metrology Along Orthogonal Directions[R]. Pattern Recognition (ICPR), 2010 20th International Conference on.Page(s): 1658 – 1661.
[7] Tony Scoleri. Video Metrology without the Image-to-Ground Homography[R]. DICTA, Int. Conf., pages 335 – 342, 2010.
[8] 王荣本,李斌,储江伟,纪寿文.公路上基于车载单目机器视觉的前方车距测量方法的研究[J].公路交通科技.2001.12:94-98.
[9] J C Aparicio Femandes, J A B Campos Neves. Angle Invariance for Distance Measurements Using a Single Camera. Industrial Electronics[J], 2006 IEEE International Symposium on .Page(s): 676 – 680.
[10] McLean, G F, Kotturi D.Vanishing Point Detection by Line Clustering[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on Page(s): 1090 – 1095,1995.
[11] Qiang He, Chu C-H H. An Efficient Vanishing Point Detection by Clustering on the Normalized Unit Sphere[R]. Computer Architecture for Machine Perception and Sensing, 2006. International Workshop on . Page(s): 203 – 207.
[12]Kogan H, Maurer R, Keshet R. Vanishing Points Estimation by Self-Similarity[R]. Computer Vision and Pattern Recognition, 2009. IEEE Conference on , Page(s): 755 - 761
[13]Xu-Cheng Yin,Hong-Wei Hao,Jun Sun, Naoi S. Robust Vanishing Point Detection for MobileCam-Based Documents[R]. Document Analysis and Recognition , 2011 International Conference on Page(s): 136 – 140.
[14] PETS 2007 Benchmark Data.http://www.cvg.rdg.ac.uk/PETS2007/S00-NO_DEFINED_BEHAVIOUR/S0.01000.cam3.jpeg.
[15] Tsai Roger Y. A Versatile Camera Calibration Technique forHigh-Accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses[J]. IEEE Journal ofRobotics and Automation, 1987, RA-3(4).
[16] Zhang Zhengyou. A Flexible New Technique for Camera Calibration[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.