数据结构（七）树

数据结构（7）树
1 前言

    今天我们来学习一下树的简单概念和结构。

2 详述2.1 树的定义

    数（Tree）是n（n>=0）个结点的有限集。n=0时称为空树。在任意一棵非空树中:(1)有且仅有一个特定得称为根（Root）的结点；（2）当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1，T2，。。。，Tn。其中每一个集合本身又是一棵树，并且称为根的子树（SubTree）。

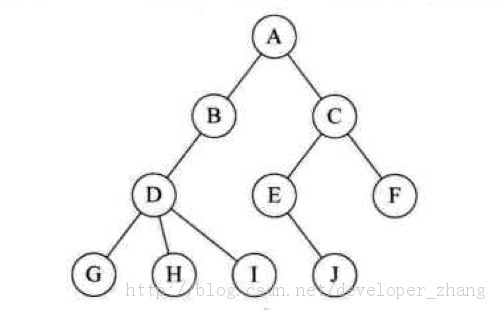
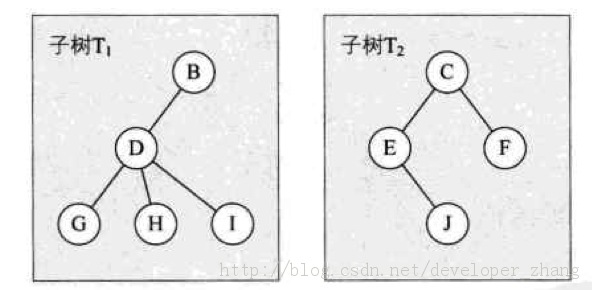
子树：

2.1.1 结点分类

结点拥有的子树数称为结点的度（Degree）。度为0的结点称为叶结点（Leaf）或者终端结点；度不为0的结点称为非终端结点或者分支结点。除了根结点之外，分支结点也称为内部结点。树的度内各个结点的度的最大值。  

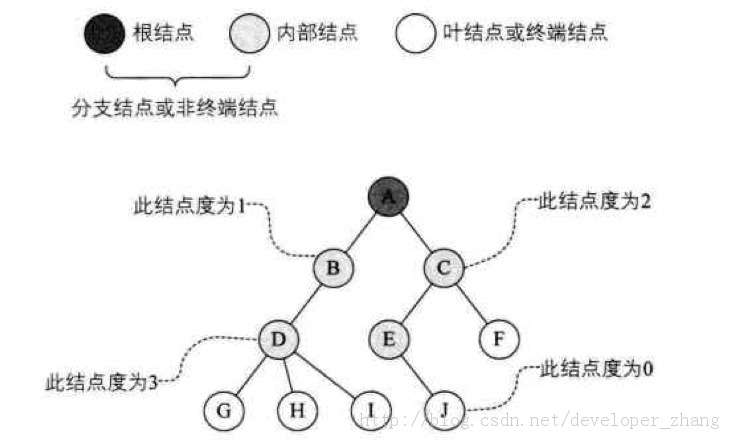
如图：这棵树的结点的度的最大值为结点D的度为3，所以树的度也为3。

2.1.2 结点间的关系

结点的子树的根称为该结点的孩子（Child），相应的，该结点称为孩子的双亲（Parent）。同一个双亲的孩子之间互称兄弟（Sibling）。

结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中的任意结点都称为该结点的子孙。

2.1.3 树的其他概念

树中结点的最大层称为树的深度（Depth）或者高度。

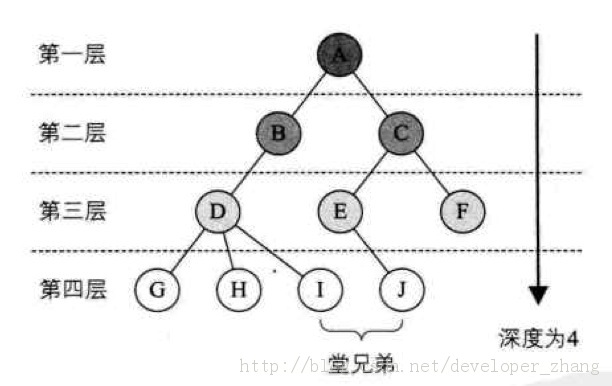
如果将树中结点的各子树看成从左到右是有次序的，不能互换的，则称该树为有序树，否则则为无序树。

森林（Forest）是m（m>=0）棵互不相交的树的集合。

2.1.4 线性表和树结构对比

2.2 树的抽象数据类型

其中data是数据域，存储结点的数据信息。而parent是指针域，存储该结点的双亲在数组中的下标。
结构定义代码：

我们约定根结点的位置域设置为-1。
存储结构的设计是一个非常灵活的过程。一个存储结构设计的是否合理，取决于基于该存储结构的元算是否适合，是否方便，时间复杂度好不好等。
2.3.2 孩子表示法
每个结点有多个指针域，其中每一个指针指向一颗子树的根结点，我们把这种方法叫做多重链表表示法。
具体办法：把每个结点的孩子结点排列起来，以单链表做存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进入一个一维数组中。
为此我们设计两种结点结构，一个是孩子链表的孩子结点：
其中child是数据域，用来存储某个结点在表头数组中的下标。next是指针域，用来存储指向某结点的下一个孩子结点的指针。
另一个是表头数组的表头结点：
其中data是数据域，存储某结点的数据信息。firstchild是头指针，存储该结点的孩子链表的头指针。
3 结语
    以上是所有内容，希望对大家有所帮助。
 

 

查看更多 下一篇