SVG中以任意直线为对称轴的镜像变换及其矩阵
直线一般方程为 A x + B y + C = 0
则以该直线为对称轴,做镜像变换的矩阵为:
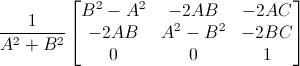
任意点P(x,y)变换后的新坐标Q(x',y')的坐标为:
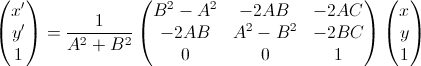
SVG中的直线通常是以坐标轴形式或者是两点形式表示的。
如果是以两点线段形式表示的,需要先求出直线方程的系数。
两点(x1,y1),(x2,y2)确定的直线方程为:
(y1-y2)*x + (x2-x1)*y + (x1*y2-x2*y1) = 0
系数分别为 A=(y1-y2), B=(x2-x1), C=(x1*y2-x2*y1)
示例SVG文件: