TOJ 2732存钱计划（三）（单源最短路）
时间限制(普通/Java):1000MS/30000MS 运行内存限制:65536KByte描述
TZC的店铺比较多，上次WY随便走只要能走到就行，现在他学聪明了。WY去买东西的话，确定一家店以后，当然他先要想想怎么样走到那家店走的路最少。店与店之间是有走的方向的，从店A到店B可以，店B到店A未必可以。店与店之间是有一定距离的。
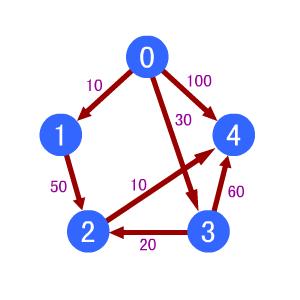
上面就是路线，为方便起见，店铺都用数字表示，0表示WY的起点，店与店之间以及起点与店距离用d表示。WY从0开始到4店铺 那么最短路线为0-->3-->2-->4 总长为 60。
如果从0店铺开始到1店铺最短路线只有0-->1 总长 10。
当然也有可能没有路的情况。
输入
输入有多组测试数据。
每组数据的第一行为整数n（n<=10），表示店铺总数。所有店铺的编号为0~n-1。
接下来有若干行，每行为3个整数
a b t
表示a编号的店铺走向b编号的店铺之间的一条路径，长度为t。0<=a，b<n（为有向路径，不能反向行走）。
当a b t的值为0 0 0 表示店铺之间的路径输入完毕，不做任何处理。
最后一行输入店铺的编号k（k<n）
输入n为0时表示结束程序。
输出
输出从店铺0到k店铺的最短路线的长度。如果没有路的话，输出 NO WAY!
样例输入
50 1 100 3 300 4 1001 2 502 4 103 2 203 4 600 0 0450 1 102 0 500 3 100 0 020
样例输出
60NO WAY!
提示
简单最短路径问题
#include <iostream>#include <cstdio>#include <cstring>#include <algorithm>#include <vector>#include <queue>using namespace std;const int INF = 0x7fffffff;const int maxn = 12;int g[maxn][maxn];int d[maxn];bool vis[maxn];int gn;void init() { int i, j; for(i = 0; i < gn; i++) { for(j = 0; j < gn; j++) { if(i == j) { g[i][j] = 0; } else { g[i][j] = INF; } } }}void dijkstra() { int i, j; for(i = 0; i < gn; i++) d[i] = INF; d[0] = 0; memset(vis, 0, sizeof(vis)); for(i = 0; i < gn; i++) { int mark = -1, mindis = INF; for(j = 0; j < gn; j++) { if(!vis[j] && d[j] < mindis) { mindis = d[j]; mark = j; } } if(mark == -1) break; vis[mark] = true; // printf("mark = %d\n", mark); for(j = 0; j < gn; j++) { if(!vis[j] && d[mark] != INF && g[mark][j] != INF) { d[j] = min(d[j], d[mark] + g[mark][j]); // printf("d[%d] = %d\n", j, d[j]); } } }}int main(){ int x, y, w; while(scanf("%d", &gn) != EOF && gn) { init(); while(scanf("%d%d%d", &x, &y, &w)==3) { if(x==0 && y==0 && w==0) break; if(g[x][y] > w) {//处理重边. g[x][y] = w; } } dijkstra(); int t; scanf("%d", &t); if(d[t]==INF) { printf("NO WAY!\n"); } else { printf("%d\n", d[t]); } } return 0;}