数学黑洞(三)角谷猜想
角谷猜想也叫考拉兹猜想或者3n+1猜想。在1960年代,日本人角谷静夫研究过这个猜想。在1930年代,德国汉堡大学的学生考拉兹,也曾经研究过这个猜想。但这猜想到目前,仍没有任何进展。这个猜想是指对于每一个正整数,如果它是奇数,则对它乘3再加1,如果它是偶数,则对它除以2,如此循环,最终都能够得到1。
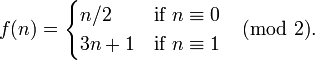
如n = 6,根据上述数式,得出 6→3→10→5→16→8→4→2→1
此猜想的程序验证:
代码清单:
#include<stdio.h>int main(){ int n,count=0; printf("Please enter number:"); scanf("%d",&n); do{ if(n & 1 == 1) { n=n*3+1; printf("[%d]:%d*3+1=%d\n",++count,(n-1)/3,n); } else { n/=2; printf("[%d]: %d/2=%d\n",++count,2*n,n); } }while(n!=1);}目前已经有分布式计算在进行验证。已验证到 5 × 260 = 5,764,607,523,034,234,880,也仍未有找到例外的情况。但是这并不能够证明对于任何大小的数,这猜想都能成立.
考拉兹曾经的学生Gerhard Opfer在《Mathematics of Computation》上发表了一篇论文,宣称证明了角谷猜想。
链接:http://preprint.math.uni-hamburg.de/public/papers/hbam/hbam2011-09.pdf
==================================================================================================
作者:nash_ 欢迎转载,与人分享是进步的源泉!
转载请保留原文地址:http://blog.csdn.net/nash_/article/details/8547383
===================================================================================================