学习Topic Model(主题模型)--Latent Dirichlet Allocation(LDA) 的一些摘要
主题模型是文本挖掘领域非常流行的方法,在文档分类、聚类中都 有大量的应用。实际上,LDA的训练过程很简单,只需要简单的计算就可以得到结果。
Blei (2003)原始的LDA论文中使用的是变分法推导,用EM算法求解。方法比较难以理解,并且EM算法可能求解到的是局部最优解。由于现在基本都是用Gibbs Sampling的方法求解,我也主要阅读的是Gibbs方面的论文。
为了看懂LDA的论文,我们必须先明白两个分布:多项式分布和Dirichlet分布。
多项式分布:一般的多项式分布是把分布看着是组合的形式,见公式。
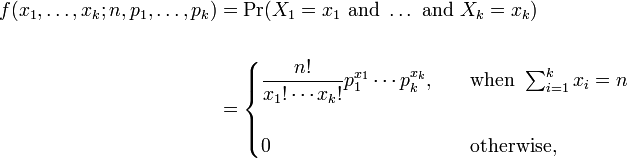
而在LDA相关论文,我们把主题产生词的分布看成是排列的方式,因此没有n!/x1!……xk! 这部分。
Dirichlet分布:文档产生主题的分布,主题产生词的分布,都是dirichlet分布。
共轭分布的概念:分布的分布就是共轭分布。dirichlet分布是多项式分布的共轭分布。
为了理解Dirichlet,请看一个关于骰子的例子【参考http://wenku.baidu.com/view/0492cdc4bb4cf7ec4afed0a7.html】:假设我们在和一个不老实的人玩掷骰子游戏。按常理我们觉得骰子每一面出现的几率都是1/6,但是掷骰子的人连续掷出6,这让我们觉得骰子被做了手脚,而这个骰子出现6的几率更高。而我们又不确定这个骰子出现6的概率到底是多少,所以我们猜测有50%的概率是:6出现的概率2/7,其它各面1/7;有25%的概率是:6出现的概率3/8,其它各面1/8;还有25%的概率是:每个面出现的概率都为1/6,也就是那个人没有作弊,走运而已。用图表表示如下:
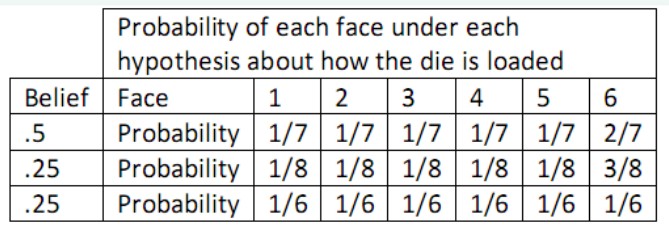
我们所猜测的值,如果设为X的话,则表示X的最自然的分布便是Dirichlet distribution。设随机变量X服从Dirichlet分布,简写为Dir(α),即X~Dir(α)。Α是一个向量,表示的是某个事件出现的次数。比如对于上例,骰子的可能输出为{1,2,3,4,5,6},假设我们分别观察到了5次1~5,10次6,那么α = {5,5,5,5,5,10}。X则表示上例中的各种概率组合,比如{1/7,1/7,1/7, 1/7,1/7,2/7};{1/8, 1/8, 1/8, 1/8, 1/8, 3/8};{1/6, 1/6, 1/6, 1/6, 1/6, 1/6},那么P(X)则表示了该概率组合出现的概率,也就是概率的概率。 以下是公式:
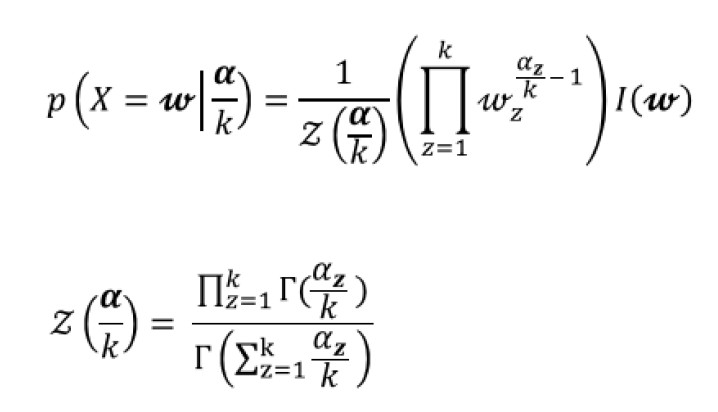
明白这两个分布之后,理解LDA的核心思想就简单了:
这里有两个多项式分布,第一每个文档的主题分布是多项式分布;每个主题下词的分布也是多项式分布。而每个多项式分布的概率满足Dirichlet分布。
这里的多项式分布是把主题或者词看着排列,即有序的。
真正计算求解我们需要明白Gibbs Sampling。对于Gibbs采样,我们还需要知道马尔可夫特性,即采样只与t-1个时刻有关系。
Gibbs采样的流程:
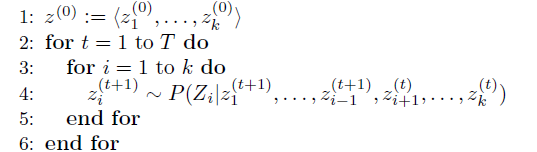
迭代T次,每迭代 一次,针对k个维度,每次更新一个维度。
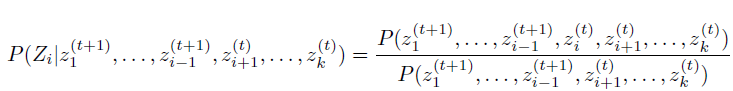
注意右边分子的上标(t+1)和(t)表示时间点,Zi前面的维度都已经更新,所以是t+1,而Zi后面的维度还没有更更新,因此是t。
LDA计算的公式:
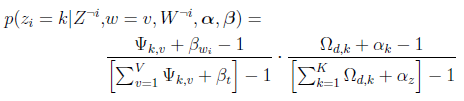
注意这里是 T(音tao)函数化解得来的。
疑惑:为什么计算P(zi| W,alpha,belta)的时候,要用一个概率来选择究竟用那个主题?
参考文献: