KMeans和KMedoid 的Matlab实现
KMeans和KMedoid算法是聚类算法中比较普遍的方法,本文讲了其原理和matlab中实现的代码。
1.目标:
找出一个分割,使得距离平方和最小
2.K-Means算法:
1. 将数据分为k个非空子集
2. 计算每个类中心点(k-means中用所有点的平均值,K-medoid用离该平均值最近的一个点)center
3. 将每个object聚类到最近的center
4. 返回2,当聚类结果不再变化的时候stop
复杂度:
O(kndt)
-计算两点间距离:d
-指定类:O(kn) ,k是类数
-迭代次数上限:t
3.K-Medoids算法:
1. 随机选择k个点作为初始medoid
2.将每个object聚类到最近的medoid
3. 更新每个类的medoid,计算objective function
4. 选择最佳参数
4. 返回2,当各类medoid不再变化的时候stop
复杂度:
O((n^2)d)
-计算各点间两两距离O((n^2)d)
-指定类:O(kn) ,k是类数
4.特点:
-聚类结果与初始点有关(因为是做steepest descent from a random initial starting oint)
-是局部最优解
-在实际做的时候,随机选择多组初始点,最后选择拥有最低TSD(Totoal Squared Distance)的那组
===================
下面是我用matlab上的实现:
说明:fea为训练样本数据,gnd为样本标号。算法中的思想和上面写的一模一样,在最后的判断accuracy方面,由于聚类和分类不同,只是得到一些 cluster ,而并不知道这些 cluster 应该被打上什么标签,或者说。由于我们的目的是衡量聚类算法的 performance ,因此直接假定这一步能实现最优的对应关系,将每个 cluster 对应到一类上去。一种办法是枚举所有可能的情况并选出最优解,另外,对于这样的问题,我们还可以用 Hungarian algorithm 来求解。具体的Hungarian代码我放在了资源里,调用方法已经写在下面函数中了。下面给出Kmeans&Kmedoid主函数。
Kmeans.m 函数:
7类聚类:
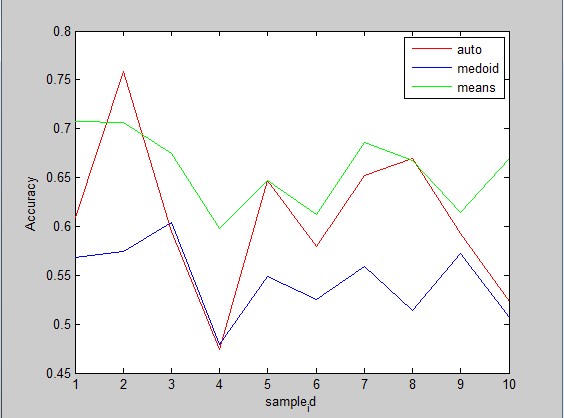
关于Machine Learning更多的学习资料与相关讨论将继续更新,敬请关注本博客和新浪微博Sophia_qing。