数据结构与算法学习6：堆排序

数据结构与算法学习六：堆排序

一.?定义?

任何关键字data[0...n]都可以组成一个完全二叉树。堆就是一种特殊的二叉树：树中任一非叶结点的关键字均大于等于(或小于等于)其左右孩子(若存在)结点的关键字。大于等于称为大根堆；小于等于称为小根堆。

?

?

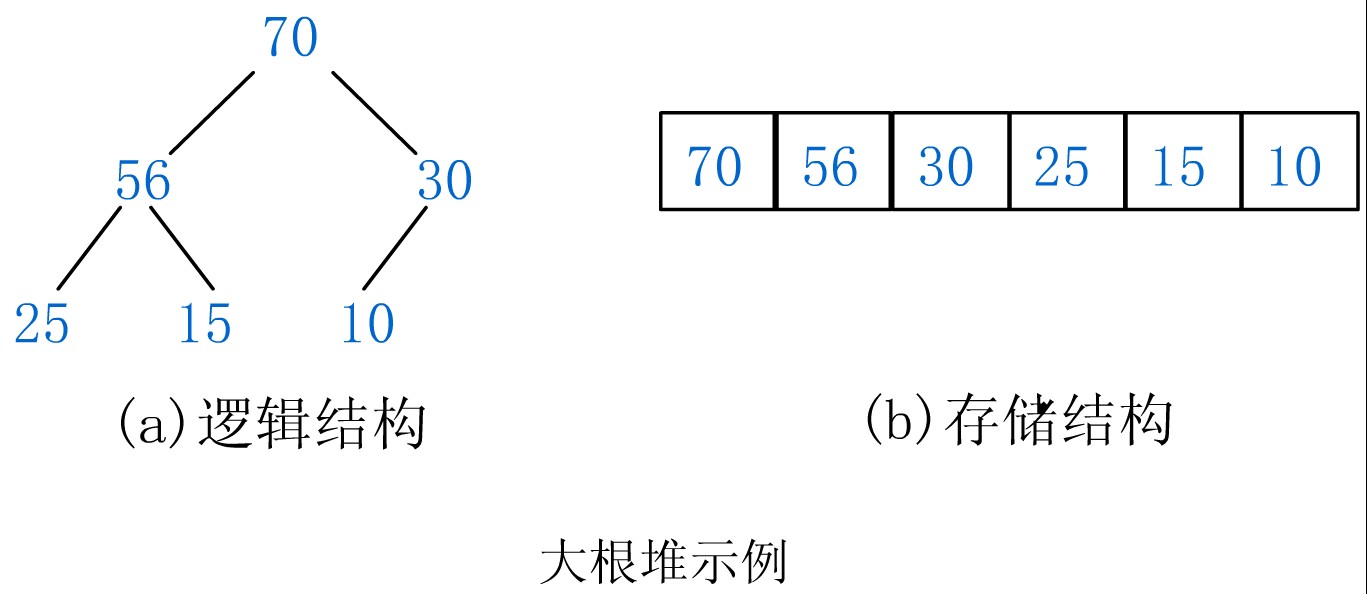
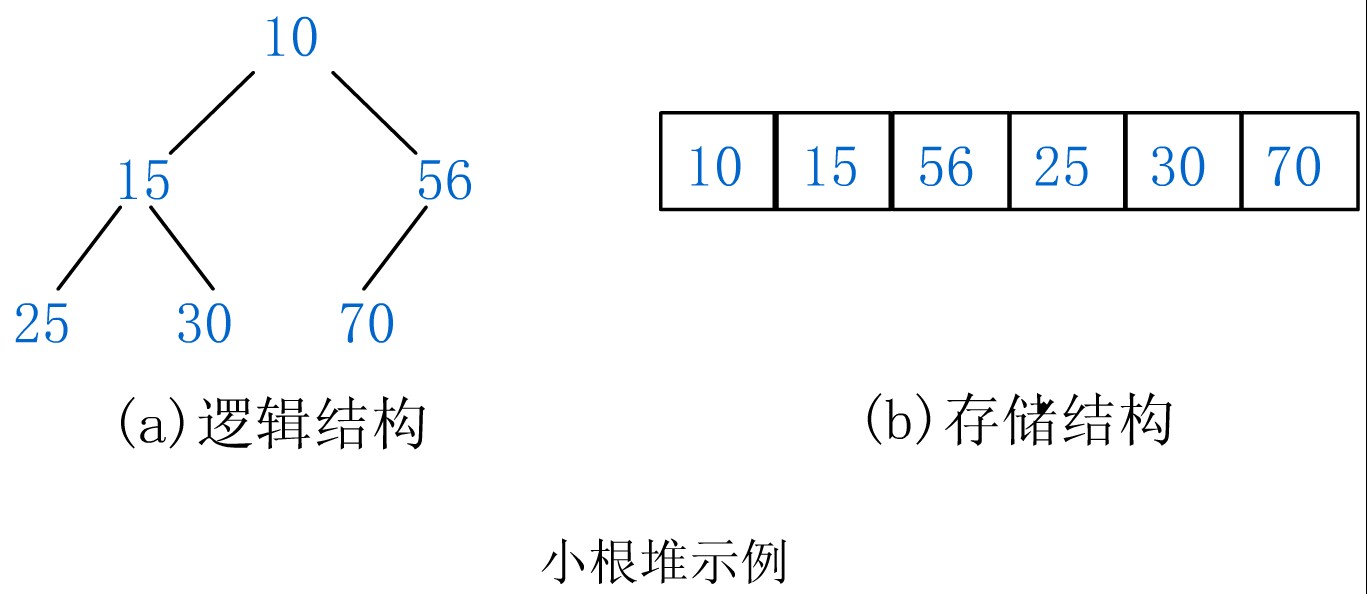
二. 排序方法(以大根堆为例)

先将初始文件data[1..n]建成一个大根堆，此堆为初始的无序区。将关键字最大的记录data[0](即堆顶)和无序区的最后一个记录data[n]交换，由此得到新的无序区data[0..n-1]和有序区data[n]，且满足data[1..n-1]≤data[n]。由于交换后新的根data[0]可能违反堆性质，故应将当前无序区data[0..n-1]调整为堆。然后再次将data[1..n-1]中关键字最大的记录data[0]和该区间的最后一个记录data[n-1]交换，由此得到新的无序区data[0..n-2]和有序区data[n-1..n]，且仍满足关系data[0..n-2]≤data[n-1..n]，同样要将data[0..n-2]调整为堆...直到无序区只有一个元素为止。

三. 动画演示

???? http://student.zjzk.cn/course_ware/data_structure/web/flashhtml/duipaixu.htm

?

四. Java代码

?

    private static int parentIdx(int childIdx) {          return (childIdx - 1) / 2;  //索引从0开始, 注意childIdx=0时返回0      }        private static int leftChildIdx(int parentIdx) {          return parentIdx*2 + 1;      }        /**      * 构建大顶堆.      */      private static void buildMaxHeap(int[] datas) {          int lastIdx = datas.length -1;          for(int i=parentIdx(lastIdx); i>=0; i--) {   //几个父节点            int k = i;           //当前父节点k=i            while(leftChildIdx(k) <= lastIdx) {                  int j = leftChildIdx(k);                  if(j < lastIdx) {    //有两个孩子                      if(datas[j] <= datas[j+1]) { //右孩子比较大, 选择大的                          j++;                      }                  }                    if(datas[k] >= datas[j]) {    //父的比较大                      break;                  } else {                      SortUtil.swap(datas, k, j);                      k = j;            //父节点重新赋值为原父节点的左孩子节点或者右孩子节点                }              }          }      }        /**      * 堆顶改变, 要维护大顶堆.      */      private static void maintainMaxHeap(int[] datas, int lastIdx) {          int k = 0;          while(k <= parentIdx(lastIdx)) {              int j = leftChildIdx(k);              if(j < lastIdx) {    //有两个孩子                  if(datas[j] <= datas[j+1]) { //j+1 比较大, 选择大的                      j++;                  }              }              if(datas[k] < datas[j]) {    //父结点比较小                  SortUtil.swap(datas, k, j);                  k = j;              } else {                  break;              }        }      }        public static int[] sort(int[] datas) {          buildMaxHeap(datas);          int lastIdx = datas.length - 1;          while(lastIdx > 0) {              SortUtil.swap(datas, 0, lastIdx);               lastIdx--;              if(lastIdx > 0) {                  maintainMaxHeap(datas, lastIdx);              }          }          return datas;      }  

?

?

五.时间复杂度和稳定性

堆排序的时间，主要由建立初始堆和反复重建堆这两部分的时间开销构成。??　? 堆排序的最坏时间复杂度为O(nlgn)。堆排序的平均性能较接近于最坏性能。由于建初始堆所需的比较次数较多，所以堆排序不适宜于记录数较少的文件。堆排序是就地排序，辅助空间为O(1)。堆排序是不稳定的排序方法。

?

六.堆排序和直接插入排序

???? 直接选择排序中，为了从data[0..n]中选出关键字最小的记录，必须进行n-1次比较，然后在data[2..n]中选出关键字最小的记录，又需要做n-2次比较。事实上，后面的n-2次比较中，有许多比较可能在前面的n-1次比较中已经做过，但由于前一趟排序时未保留这些比较结果，所以后一趟排序时又重复执行了这些比较操作。
??? 　堆排序可通过树形结构保存部分比较结果，可减少比较次数。

?