斐波那契数:动态规划法和分治法
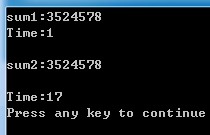
这个学期开了一门叫算法的课,为了今天的ITAT复赛,这两天研究了一下这门课。感觉算法真的是太神奇了。就比如说今天学了动态规划(小小的入门)。用它实现了斐波那契数,和原来的用分治法的一比较,差距出来了。相差十几几万倍(要算的数越大相差的倍数越多)。下面是实现:
#include <iostream>#include <ctime>using namespace std;/** 动态规划法实现*/int f(int n, int a[]){if (n < 0){return 0;}if (n == 0 || n == 1){return n;}else{/* 计算f(n-1) 与已经计算过的f(n-2)=a[n-2]*/// 如果febonacci函数中没有for语句的事先填表// 可以用a[n] = a[n-1] + a[n-2];实现动态填表return f(n-1,a) + a[n-2];}}/** 填表函数*/int febonacci(int n){int a[1000] = {0};a[0] = 0;a[1] = 1;/* 自底向上填表 */for (int i = 2; i <= n; i++){a[i] = a[i-1] + a[i-2];}int sum = f(n,a);return sum;}/** 分治法实现*/int f2(int n){if (n == 0 || n == 1){return n;}else{return f2(n-1) + f2(n-2);}}int main(){time_t begin1,end1;time_t begin2,end2;// 斐波那契数的阶数int i = 33;begin1 = time(NULL);int sum1 = 0;// 计算100万次for(int k = 0; k < 1000000; k++){sum1 = febonacci(i);}cout<<"sum1:"<<sum1<<endl;end1 = time(NULL);cout<<"Time:"<<end1 - begin1<<endl<<endl;begin2 = time(NULL);int sum2 = 0;// 计算100次for (int m = 0; m < 100; m++){sum2 = f2(i);}cout<<"sum2:"<<sum2<<endl<<endl;end2 = time(NULL);cout<<"Time:"<<end2 - begin2<<endl;return EXIT_SUCCESS;}