微软等数据结构与算法面试100题 第十九题
第十九题
题目:
定义Fibonacci数列如下:
/ 0 n=0
f(n) = 1 n=1
\ = f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:
对于解决斐波那契数列问题,目前主要有三类方法:
1,递归方法;复杂度应该是指数的。
2,非递归的方法,应该可以叫做动态规划方法。由于存在大量的重复解的问题,因此可以使用动态规划方法。复杂度为o(n)
3,化简成矩阵的叠成运算,复杂度为log(n)。原理如下图公式所示。
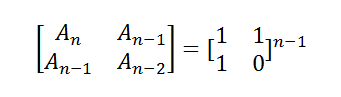
代码:
#include<iostream>using namespace std;int fibonacci(int n)//非递归的方法,复杂度为O(n){if(n==0)return 0;else if(n==1) return 1;else if(n==2) return 1;else{int *arrValue = new int[n+1];arrValue[0]=0;arrValue[1]=1;arrValue[2]=1;for(int i = 3; i <=n; i++){arrValue[i] = arrValue[i-1] + arrValue[i-2];}int value = arrValue[n];delete [] arrValue;return value;}}int recu_fibonacci(int n)//递归的方法,复杂度为指数{if(n==0)return 0;else if(n==1) return 1;else if(n==2) return 1;else return recu_fibonacci(n-1)+recu_fibonacci(n-2);}struct mat{int value1 ;int value2 ;int value3 ;int value4 ;};void matSquare(mat struct_1, mat struct_2, mat &ss){ ss.value1 = struct_2.value1*struct_1.value1+struct_2.value2*struct_1.value3;ss.value2 = struct_2.value1*struct_1.value2+struct_2.value2*struct_1.value4;ss.value3 = struct_2.value3*struct_1.value1+struct_2.value4*struct_1.value3;ss.value4 = struct_2.value3*struct_1.value2+struct_2.value4*struct_1.value4;}void unitMatrix_n(int n, mat &ss){//[1, 1 ;1, 0]的n次方mat unitMatrix;unitMatrix.value1 = 1;unitMatrix.value2 = 1;unitMatrix.value3 = 1;unitMatrix.value4 = 0;ss = unitMatrix;if(n==1) return;else{mat currentMatrix, currentMatrix1, currentMatrix2;if(n%2==0){unitMatrix_n(n/2, currentMatrix1);matSquare(currentMatrix1, currentMatrix1, currentMatrix);}else{unitMatrix_n(n-1, currentMatrix1);matSquare(currentMatrix1, unitMatrix, currentMatrix);}ss = currentMatrix;}}int recu_fibonacci_logn(int n)//矩阵叠乘,复杂度为log(n){if(n==0)return 0;else if(n==1) return 1;else{mat ss;unitMatrix_n(n-1,ss);return ss.value1;}}int main(){cout<<recu_fibonacci(0)<<endl;cout<<recu_fibonacci(1)<<endl;cout<<recu_fibonacci(2)<<endl;cout<<recu_fibonacci(3)<<endl;cout<<recu_fibonacci(6)<<endl;cout<<fibonacci(0)<<endl;cout<<fibonacci(1)<<endl;cout<<fibonacci(2)<<endl;cout<<fibonacci(3)<<endl;cout<<fibonacci(6)<<endl;cout<<recu_fibonacci_logn(0)<<endl;cout<<recu_fibonacci_logn(1)<<endl;cout<<recu_fibonacci_logn(2)<<endl;cout<<recu_fibonacci_logn(3)<<endl;cout<<recu_fibonacci_logn(6)<<endl;return 0;}