微软等数据结构与算法口试100题第十五题

微软等数据结构与算法面试100题第十五题

第十五题

题目：

输入一颗二元查找树，将该树转换为它的镜像，

用递归和循环两种方法完成树的镜像转换。

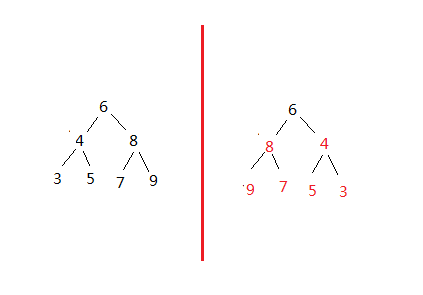
分析：

题目要求求解一个二元搜索树的镜像，用两种方法实现，递归和非递归。

首先，对于求解一个二元搜索树镜像其实就是把树中的每个节点的左右子树调换了即可，因此思路就是周游一个树的所有节点，对于每个节点其左右子树对调。

周游一个树主要有两种方法，深度优先的周游和广度优先的周游。分别使用了栈stack和队列queue。其中深度优先周游可以使用递归的方法和非递归的方法。广度优先使用了

非递归的方法。这里这几种方法都可以实现题目的要求。

在这里，我们选用了比较栈来实现递归和非递归的两种方法。

递归方法代码：

#include<iostream>#include<stack>using namespace std; struct node{node * leftNode;node * rightNode;int value;};class BSTree{private:node * pTree;public:BSTree(){pTree= NULL;};void addNodeBST(const int item, node * &root);void inOrder(node * root);node * Root(){return pTree;};void mirrorBSTree(node * &root);};void BSTree::addNodeBST(const int item, node * &root){node * pTemp;if(NULL==root){pTemp = new struct node();pTemp->leftNode = NULL;pTemp->rightNode = NULL;pTemp->value = item;root = pTemp;}else{if(item < root->value){addNodeBST(item,root->leftNode);}else if(item > root ->value){addNodeBST(item,root->rightNode);}else{cout<<"节点已经存在"<<" "<<endl;return;}}}void BSTree::inOrder(node * root){if(NULL!=root){inOrder(root->leftNode);cout<<root->value<<" "<<endl;inOrder(root->rightNode);}}void BSTree::mirrorBSTree(node * & root){if(NULL==root){return;}node * pTemp;//递归遍历//if(NULL!=root)//{//pTemp = root->leftNode;//root->leftNode = root->rightNode;//root->rightNode = pTemp;//mirrorBSTree(root->leftNode);//mirrorBSTree(root->rightNode);//}//非递归二叉树周游，可以使用深度优先也可以使用广度优先，这里采用了深度优先stack<node *> nodeStack;node * pStackTemp = root;node * pExTemp;nodeStack.push(NULL); //压入监视哨while(pStackTemp){pExTemp = pStackTemp->leftNode;pStackTemp->leftNode = pStackTemp->rightNode;pStackTemp->rightNode = pExTemp;if(NULL!=pStackTemp->leftNode){nodeStack.push(pStackTemp->leftNode);}if(NULL!=pStackTemp->rightNode){nodeStack.push(pStackTemp->rightNode);}if(!nodeStack.empty()){pStackTemp = nodeStack.top();nodeStack.pop();}}}int main(){BSTree a; node * head = a.Root();a.addNodeBST(6,head);a.addNodeBST(8,head);a.addNodeBST(7,head);a.addNodeBST(9,head);a.addNodeBST(4,head);a.addNodeBST(5,head);a.addNodeBST(3,head);a.inOrder(head);a.mirrorBSTree(head);a.inOrder(head);return 0;}