遗传算法原理与应用详解
遗传算法 ( GA , Genetic Algorithm ) ,也称进化算法 。 遗传算法是受达尔文的进化论的启发,借鉴生物进化过程而提出的一种启发式搜索算法。因此在介绍遗传算法前有必要简单的介绍生物进化知识。
一.进化论知识作为遗传算法生物背景的介绍,下面内容了解即可:
种群(Population):生物的进化以群体的形式进行,这样的一个群体称为种群。
个体:组成种群的单个生物。
基因 ( Gene ) :一个遗传因子。
染色体 ( Chromosome ) :包含一组的基因。
生存竞争,适者生存:对环境适应度高的、牛B的个体参与繁殖的机会比较多,后代就会越来越多。适应度低的个体参与繁殖的机会比较少,后代就会越来越少。
遗传与变异:新个体会遗传父母双方各一部分的基因,同时有一定的概率发生基因变异。
简单说来就是:繁殖过程,会发生基因交叉( Crossover ) ,基因突变 ( Mutation ) ,适应度( Fitness )低的个体会被逐步淘汰,而适应度高的个体会越来越多。那么经过N代的自然选择后,保存下来的个体都是适应度很高的,其中很可能包含史上产生的适应度最高的那个个体。
二.遗传算法思想 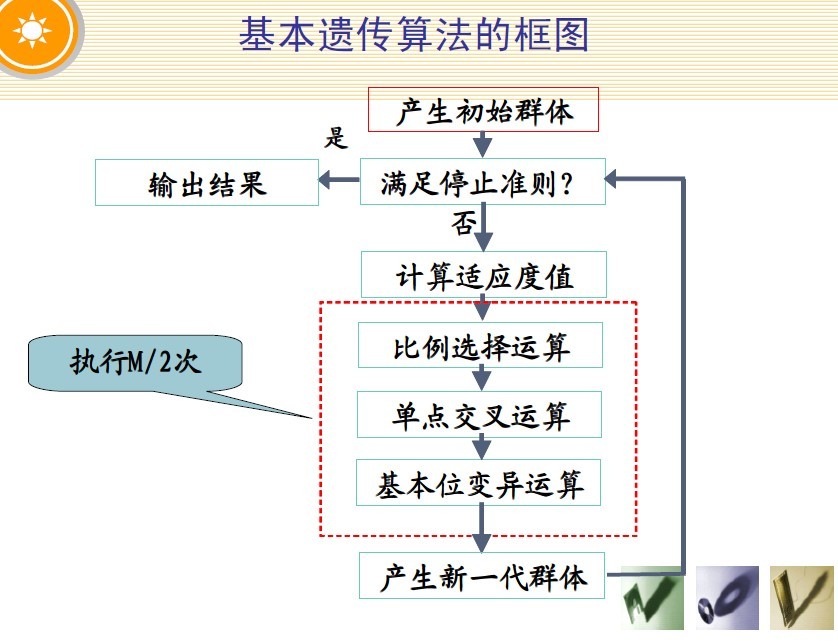
借鉴生物进化论,遗传算法将要解决的问题模拟成一个生物进化的过程,通过复制、交叉、突变等操作产生下一代的解,并逐步淘汰掉适应度函数值低的解,增加适应度函数值高的解。这样进化N代后就很有可能会进化出适应度函数值很高的个体。
举个例子,使用遗传算法解决“0-1背包问题”的思路:0-1背包的解可以编码为一串0-1字符串(0:不取,1:取) ;首先,随机产生M个0-1字符串,然后评价这些0-1字符串作为0-1背包问题的解的优劣;然后,随机选择一些字符串通过交叉、突变等操作产生下一代的M个字符串,而且较优的解被选中的概率要比较高。这样经过G代的进化后就可能会产生出0-1背包问题的一个“近似最优解”。
编码:需要将问题的解编码成字符串的形式才能使用遗传算法。最简单的一种编码方式是二进制编码,即将问题的解编码成二进制位数组的形式。例如,问题的解是整数,那么可以将其编码成二进制位数组的形式。将0-1字符串作为0-1背包问题的解就属于二进制编码。
遗传算法有3个最基本的操作:选择,交叉,变异。
选择:选择一些染色体来产生下一代。一种常用的选择策略是 “比例选择”,也就是个体被选中的概率与其适应度函数值成正比。假设群体的个体总数是M,那么那么一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) ) 。比例选择实现算法就是所谓的“轮盘赌算法”( Roulette Wheel Selection ) ,轮盘赌算法的一个简单的实现如下:
轮盘赌算法/** 按设定的概率,随机选中一个个体* P[i]表示第i个个体被选中的概率*/int RWS(){ m = 0; r =Random(0,1); //r为0至1的随机数 for(i=1;i<=N; i++) { /* 产生的随机数在m~m+P[i]间则认为选中了i * 因此i被选中的概率是P[i] */ m = m + P[i]; if(r<=m) return i; }}交叉(Crossover):2条染色体交换部分基因,来构造下一代的2条新的染色体。例如:
交叉前:
00000|011100000000|10000
11100|000001111110|00101
交叉后:
00000|000001111110|10000
11100|011100000000|00101
染色体交叉是以一定的概率发生的,这个概率记为Pc 。
变异(Mutation):在繁殖过程,新产生的染色体中的基因会以一定的概率出错,称为变异。变异发生的概率记为Pm 。例如:
变异前:
000001110000000010000
变异后:
000001110000100010000
适应度函数 ( Fitness Function ):用于评价某个染色体的适应度,用f(x)表示。有时需要区分染色体的适应度函数与问题的目标函数。例如:0-1背包问题的目标函数是所取得物品价值,但将物品价值作为染色体的适应度函数可能并不一定适合。适应度函数与目标函数是正相关的,可对目标函数作一些变形来得到适应度函数。
三.基本遗传算法的代码
说明:求取x[1]^2-x[1]*x[2]+x[3]的最大值,工程下的gadata.txt里面每一行分别代表x[1]、x[2]和x[3]的范围,输出结果在工程下的galog.txt里面。
初始种群规模、最大迭代次数、交叉概率、变异概率等详见代码。
/**************************************************************************//* This is a simple genetic algorithm implementation where the *//* evaluation function takes positive values only and the *//* fitness of an individual is the same as the value of the *//* objective function *//**************************************************************************/#include <stdio.h>#include <stdlib.h>#include <math.h>/* Change any of these parameters to match your needs */#define POPSIZE 50 /* population size */#define MAXGENS 1000 /* max. number of generations */#define NVARS 3 /* no. of problem variables */ //gadata.txt中有3行数据,可以给定3组不同范围的数据#define PXOVER 0.8 /* probability of crossover */#define PMUTATION 0.15 /* probability of mutation */#define TRUE 1#define FALSE 0int generation; /* current generation no. */int cur_best; /* best individual */FILE *galog; /* an output file */struct genotype /* genotype (GT), a member of the population */{double gene[NVARS]; /* a string of variables */ double fitness; /* GT's fitness */double upper[NVARS]; /* GT's variables upper bound */double lower[NVARS]; /* GT's variables lower bound */double rfitness; /* relative fitness */double cfitness; /* cumulative fitness */};struct genotype population[POPSIZE+1]; /* population */struct genotype newpopulation[POPSIZE+1]; /* new population; *//* replaces the *//* old generation *//* Declaration of procedures used by this genetic algorithm */void initialize(void);double randval(double, double);void evaluate(void);void keep_the_best(void);void elitist(void);void select(void);void crossover(void);void Xover(int,int);void swap(double *, double *);void mutate(void);void report(void);/***************************************************************//* Initialization function: Initializes the values of genes *//* within the variables bounds. It also initializes (to zero) *//* all fitness values for each member of the population. It *//* reads upper and lower bounds of each variable from the *//* input file `gadata.txt'. It randomly generates values *//* between these bounds for each gene of each genotype in the *//* population. The format of the input file `gadata.txt' is *//* var1_lower_bound var1_upper bound *//* var2_lower_bound var2_upper bound ... *//***************************************************************/void initialize(void){FILE *infile;int i, j;double lbound, ubound;if ((infile = fopen("gadata.txt","r"))==NULL){fprintf(galog,"\nCannot open input file!\n");exit(1);}/* initialize variables within the bounds */for (i = 0; i < NVARS; i++){fscanf(infile, "%lf",&lbound);fscanf(infile, "%lf",&ubound);for (j = 0; j < POPSIZE; j++){population[j].fitness = 0;population[j].rfitness = 0;population[j].cfitness = 0;population[j].lower[i] = lbound;population[j].upper[i]= ubound;population[j].gene[i] = randval(population[j].lower[i],population[j].upper[i]);}}fclose(infile);}/***********************************************************//* Random value generator: Generates a value within bounds *//***********************************************************/double randval(double low, double high){double val;val = ((double)(rand()%1000)/1000.0)*(high - low) + low;return(val);}/*************************************************************//* Evaluation function: This takes a user defined function. *//* Each time this is changed, the code has to be recompiled. *//* The current function is: x[1]^2-x[1]*x[2]+x[3] *//*************************************************************/void evaluate(void){int mem;int i;double x[NVARS+1];for (mem = 0; mem < POPSIZE; mem++){for (i = 0; i < NVARS; i++) x[i+1] = population[mem].gene[i];population[mem].fitness = (x[1]*x[1]) - (x[1]*x[2]) + x[3]; //利用自定义函数求适应度}}/***************************************************************//* Keep_the_best function: This function keeps track of the *//* best member of the population. Note that the last entry in *//* the array Population holds a copy of the best individual *//***************************************************************/void keep_the_best(){int mem;int i;cur_best = 0; /* stores the index of the best individual */for (mem = 0; mem < POPSIZE; mem++){if (population[mem].fitness > population[POPSIZE].fitness){ cur_best = mem; population[POPSIZE].fitness = population[mem].fitness; //population[50]存放最好的fitness}}/* once the best member in the population is found, copy the genes */for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[cur_best].gene[i]; //population[50]存放最好的gene}/****************************************************************//* Elitist function: The best member of the previous generation *//* is stored as the last in the array. If the best member of *//* the current generation is worse then the best member of the *//* previous generation, the latter one would replace the worst *//* member of the current population *//****************************************************************/void elitist(){int i;double best, worst; /* best and worst fitness values */int best_mem, worst_mem; /* indexes of the best and worst member */best = population[0].fitness;worst = population[0].fitness;for (i = 0; i < POPSIZE - 1; ++i){if(population[i].fitness > population[i+1].fitness){ if (population[i].fitness >= best){best = population[i].fitness;best_mem = i;} if (population[i+1].fitness <= worst){worst = population[i+1].fitness;worst_mem = i + 1;}}else{ if (population[i].fitness <= worst){worst = population[i].fitness;worst_mem = i;} if (population[i+1].fitness >= best){best = population[i+1].fitness;best_mem = i + 1;}}}/* if best individual from the new population is better than *//* the best individual from the previous population, then *//* copy the best from the new population; else replace the *//* worst individual from the current population with the *//* best one from the previous generation */if (best >= population[POPSIZE].fitness) {for (i = 0; i < NVARS; i++)population[POPSIZE].gene[i] = population[best_mem].gene[i];population[POPSIZE].fitness = population[best_mem].fitness; }else {for (i = 0; i < NVARS; i++)population[worst_mem].gene[i] = population[POPSIZE].gene[i];population[worst_mem].fitness = population[POPSIZE].fitness; }}/**************************************************************//* Selection function: Standard proportional selection for *//* maximization problems incorporating elitist model - makes *//* sure that the best member survives *//**************************************************************/void select(void){int mem, i,j;double sum = 0;double p;/* find total fitness of the population */for (mem = 0; mem < POPSIZE; mem++){sum += population[mem].fitness;}/* calculate relative fitness */for (mem = 0; mem < POPSIZE; mem++){population[mem].rfitness = population[mem].fitness/sum; //计算相对fitness}/* calculate cumulative fitness */population[0].cfitness = population[0].rfitness;for (mem = 1; mem < POPSIZE; mem++){population[mem].cfitness = population[mem-1].cfitness + population[mem].rfitness; //计算累计fitness}/* finally select survivors using cumulative fitness. */for (i = 0; i < POPSIZE; i++){p = rand()%1000/1000.0;if (p < population[0].cfitness) newpopulation[i] = population[0]; else{ for (j = 0; j < POPSIZE;j++) if (p >= population[j].cfitness && p<population[j+1].cfitness)newpopulation[i] = population[j+1];}}/* once a new population is created, copy it back */for (i = 0; i < POPSIZE; i++)population[i] = newpopulation[i]; }/***************************************************************//* Crossover selection: selects two parents that take part in *//* the crossover. Implements a single point crossover *//***************************************************************/void crossover(void){int mem, one;int first = 0; /* count of the number of members chosen */double x;for (mem = 0; mem < POPSIZE; ++mem){x = rand()%1000/1000.0;if (x < PXOVER){ ++first; if (first % 2 == 0)Xover(one, mem); elseone = mem;}}}/**************************************************************//* Crossover: performs crossover of the two selected parents. *//**************************************************************/void Xover(int one, int two){int i;int point; /* crossover point *//* select crossover point */if(NVARS > 1){if(NVARS == 2)point = 1;elsepoint = (rand() % (NVARS - 1)) + 1;for (i = 0; i < point; i++)swap(&population[one].gene[i], &population[two].gene[i]);}}/*************************************************************//* Swap: A swap procedure that helps in swapping 2 variables *//*************************************************************/void swap(double *x, double *y){double temp;temp = *x;*x = *y;*y = temp;}/**************************************************************//* Mutation: Random uniform mutation. A variable selected for *//* mutation is replaced by a random value between lower and *//* upper bounds of this variable *//**************************************************************/void mutate(void){int i, j;double lbound, hbound;double x;for (i = 0; i < POPSIZE; i++)for (j = 0; j < NVARS; j++){ x = rand()%1000/1000.0; if (x < PMUTATION){/* find the bounds on the variable to be mutated */lbound = population[i].lower[j];hbound = population[i].upper[j]; population[i].gene[j] = randval(lbound, hbound);}}}/***************************************************************//* Report function: Reports progress of the simulation. Data *//* dumped into the output file are separated by commas *//***************************************************************/void report(void){int i;double best_val; /* best population fitness */double avg; /* avg population fitness */double stddev; /* std. deviation of population fitness */ //偏离、越轨double sum_square; /* sum of square for std. calc */double square_sum; /* square of sum for std. calc */double sum; /* total population fitness */sum = 0.0;sum_square = 0.0;for (i = 0; i < POPSIZE; i++){sum += population[i].fitness; //fitness之和sum_square += population[i].fitness * population[i].fitness; //fitness的平方和}avg = sum/(double)POPSIZE;square_sum = avg * avg * POPSIZE;stddev = sqrt((sum_square - square_sum)/(POPSIZE - 1));best_val = population[POPSIZE].fitness; //最大的fitnessfprintf(galog, "\n%5d, %6.3f, %6.3f, %6.3f \n\n", generation,best_val, avg, stddev);}/**************************************************************//* Main function: Each generation involves selecting the best *//* members, performing crossover & mutation and then *//* evaluating the resulting population, until the terminating *//* condition is satisfied *//**************************************************************/void main(void){int i;if ((galog = fopen("galog.txt","w"))==NULL){exit(1);}generation = 0;fprintf(galog, "\n generation best average standard \n");fprintf(galog, " number value fitness deviation \n");//前期三步曲initialize();evaluate();keep_the_best();//迭代筛选while(generation<MAXGENS){generation++;select();crossover();mutate();report(); //输出evaluate(); //更新适应度elitist();}fprintf(galog,"\n\n Simulation completed\n");fprintf(galog,"\n Best member: \n");for (i = 0; i < NVARS; i++){fprintf (galog,"\n var(%d) = %3.3f",i,population[POPSIZE].gene[i]);}fprintf(galog,"\n\n Best fitness = %3.3f",population[POPSIZE].fitness);fclose(galog);printf("Success\n");}/***************************************************************/四.基本遗传算法优化
精英主义选择:是基本遗传算法的一种优化。为了防止进化过程中产生的最优解被交叉和变异所破坏,可以将每一代中的最优解原封不动的复制到下一代中。
插入操作:可在3个基本操作的基础上增加一个插入操作。插入操作将染色体中的某个随机的片段移位到另一个随机的位置。