【扩展欧几里德】SGU 106
KIDx的解题报告
?
题目链接:http://acm.sgu.ru/problem.php?contest=0&problem=106
?
题意:求ax + by + c = 0在[x1, x2], [y1, y2]区间内有多少组解?
?
解析:
①令c = -c有ax + by = c,可用扩展欧几里德解方程解出特解
当然要先考虑a = 0, b = 0, c = 0的情况进行特判
例如:a = 0, b = 1, c = 3,x∈[x1, x2], y∈[3, 4]
即可得知有方程有x2-x1+1个解,因为x可以区间内任意,且y=3这个解在区间内,其他情况同理了
②然后就是关键了,用的是扩展欧几里德通解式:(设一整数k,x0为x的特解)
1、x1 <= x0+k*b <= x2
2、y0 = (c - a*x0) / b
3、y1 <= y0+k'*b <= y2
解出k和k'的范围[s, e]!
注意了,例如解x1 <= x0+k*b:
当b<0时两边同时除以b,<=要变成>=号
--->k <= (x1-x0) / b
然后最关键就是除不尽应该向什么方向舍入?
区间[s, e]的舍入方向:
正数s, e的情况: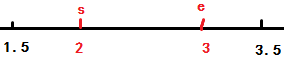
可见s = (x1-x0)/b还要+1,e直接除即可
负数s, e的情况: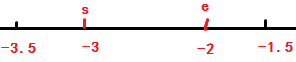
可见e = (x1-x0)/b还要-1,s直接除即可
③最后得到x的k的范围[s1, e1], y的k'的范围[s2, e2]
因为x增加必然导致y减小,所以有: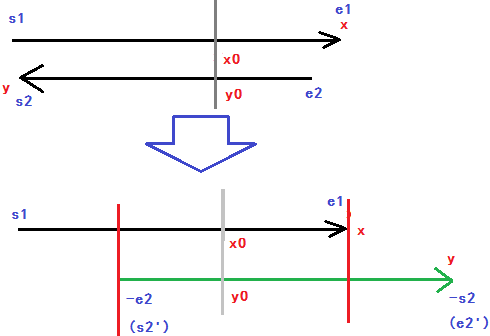
举个例子,如图所示:令-e2作为s2,令-s2作为e2,答案为[-e2, e1]
?
所以答案ans = min (e1, e2') - max (s1, s2') + 1;
#include <iostream>#include <stdio.h>#include <string>#include <cstring>#include <stdlib.h>#include <map>#include <algorithm>#include <math.h>using namespace std;#define M 1005#define LL long longLL gcd (LL a, LL b){return b ? gcd (b, a%b) : a;}void Egcd (LL a, LL b, LL &x, LL &y){if (b == 0){x = 1, y = 0;return ;}LL tp;Egcd (b, a%b, x, y);tp = x;x = y;y = tp - a/b*y;}LL cal (LL f, LL n, int key)//处理舍入问题{if (f % n == 0) return f/n;if (key == 0){if (f * n < 0) return f/n;return f/n+1;}if (f * n < 0) return f/n-1;return f/n;}LL a, b, c;LL solve (LL &x1, LL &x2, LL &y1, LL &y2){LL d, x, y, s1, e1, s2, e2;c = -c;/***********************特判***********************/if (a == 0 && b == 0 && c == 0)return (x2-x1+1) * (y2-y1+1);if (a == 0 && b == 0) return 0;if (a == 0){if (c % b != 0) return 0;y = c / b;if (y >= y1 && y <= y2) return x2 - x1 + 1;return 0;}if (b == 0){if (c % a != 0) return 0;x = c / a;if (x >= x1 && x <= x2) return y2 - y1 + 1;return 0;}/***********************特判***********************/d = gcd (a, b);if (c % d != 0) return 0;a /= d, b /= d, c /= d;Egcd (a, b, x, y);x *= c;x = (x % b + b) % b; //x的特解s1 = cal (x1-x, b, b<0);//s1e1 = cal (x2-x, b, b>0);//e1y = (c - a*x) / b; //有了x,求对应的ye2 = -cal (y1-y, a, a<0);//e2' = -s2s2 = -cal (y2-y, a, a>0);//s2' = -e2if (b < 0) s1 ^= e1, e1 ^= s1, s1 ^= e1;//b为负数,变号导致区间头尾互换if (a < 0) s2 ^= e2, e2 ^= s2, s2 ^= e2;//同理LL ans = min (e1, e2) - max (s1, s2) + 1;if (ans < 0) ans = 0;return ans;}int main(){LL x1, x2, y1, y2;while (~scanf ("%lld%lld%lld", &a, &b, &c)){scanf ("%lld%lld%lld%lld", &x1, &x2, &y1, &y2);printf ("%lld\n", solve (x1, x2, y1, y2));}return 0;}