线段树（二）——时间、空间复杂度
参考文章：
《在一维数组中以完全二叉树方式存储线段树的空间分析》 http://comzyh.tk/blog/archives/479/
《线段树简介与简单应用》http://hi.baidu.com/etwge/blog/item/c6c2dff887d2eb909f514664.html
?
我们大家存储线段树的方式无非两种：
二叉链表优点是节省空间,缺点是编程复杂度大,执行效率较低,空间复杂度为2N
在一维数组以完全二叉树方式存储线段树的编程复杂度小,执行效率较高,但浪费空间
长期以来,我和我校的OIer一直不知以一维方式存储线段树到底需要开多大的数组.今天正好有些闲暇的时间,写了个小程序,分析了下一维线段树在一维方式存储下到底需要占用多少空间.经本文所述方式计算约为4N
?
先来补习一下完全二叉树的相关知识:
完全二叉树在一维数组中这样表示:根节点为1,其左子树为2,右子树为3.
根节点为N,其左孩子为2N,右孩子为2N+1
具体实现方式可参考我的一篇题解,这里使用的就是完全二叉树方式
像线段树这样区间长度并不一定是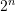
的二叉树,其占用空间为 2的(最深线段的深度)次幂,就给线段树的空间占用造成了很大的不确定性.在我们学校,关于线段树的空间占用,说法大致有以下几种
然而大家写的是后大部分都是尽量多开,对于其空间占用一直没有定论,现在我来给个定论:
先上一幅图:
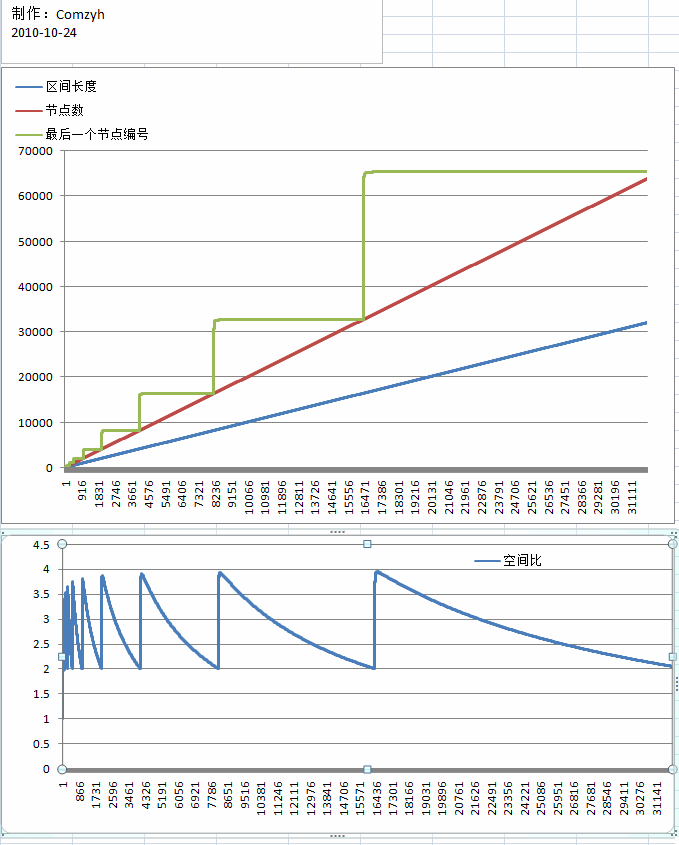
可以看到,空间复杂度其实是最好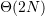
,最差是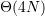
,最好情况出现在略小于
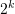附近,最坏情况出现在略大于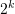附近,由此看来,我们以后存线段树大概需要开4N+100 的数组就可以了.
?
关于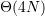，思考一下代表总区间[1,L]的线段树需要多少个节点即可（tips: 不断二分，上限是一棵满二叉树； conclusion: 空间<2^0+2^1+...+2^(1+log(L-1))=4(L-1)-1）
?
附线段树空间计算程序:
输入区间长度,他来告诉你要开多大数组.
/*注：这是一棵离散型的线段树*/#include <iostream>//#include <cstdio>//#include <cstdlib>using namespace std;struct segment { int b,e;};segment seg[5000000];int N;//线段树对应的总区间长度1,2,...,Nint Nnode;//线段树中一共有多少结点(这棵线段树基本上是平衡的二叉树，但不一定是完全二叉树)int LastNode;//线段树中最后一个结点的序号void build(int b, int e, int s);int main(){ while (1){ printf("Please Enter Interval length 请输入区间长度:\n"); scanf("%d",&N); if (N==0)return 0; Nnode=0; LastNode=0; build(1,N,1); printf("Complete binary tree, has build %d Nodes ,the last node numbered %d\n %d 最后一个节点:%d\n",Nnode,LastNode,Nnode,LastNode); //system("pause"); }}void build(int b, int e, int s){ Nnode++; if (s>LastNode) LastNode=s; seg[s].b=b; seg[s].e=e; if (b==e) return; int mid =(b+e)>>1; build(b,mid,s<<1); build(mid+1,e,(s<<1)+1);}?附线段树空间占用分析程序(打表),上面那个图的表就是它计算出来的:
/*线段树空间分析程序 Power By:Comzyh*/#include <iostream>#include <cstdio>#include <cstdlib>using namespace std;struct segment { int b,e; };segment seg[5000000];int N;int Nnode,LastNode;void build(int b, int e, int s);int main(){ freopen ("segmentCount.csv","w",stdout); int i=1; scanf("%d",&N); printf("区间长度,节点数,最后一个节点编号\n"); while (N-i>=0){ Nnode=0; LastNode=0; build(1,i,1); printf("%d,%d,%d\n",i,Nnode,LastNode); i++; } //system("pause"); }void build(int b, int e, int s){ Nnode++; if (s>LastNode) LastNode=s; seg[s].b=b; seg[s].e=e; if (b==e) return; int mid =(b+e)>>1; build(b,mid,s<<1); build(mid+1,e,(s<<1)+1); }?
然后打了个表,可以用来查询线段树空间
区间长度 ,占用空间 1:1 2:3 3:5 4:7 5:9 6:13 7:13 8:15 9:17 10:25 10:25 20:57 30:61 40:121 50:125 60:125 70:225 80:249 90:249 100:253 200:509 300:1009 400:1021 500:1021 600:2033 700:2041 800:2045 900:2045 1000:2045 2000:4093 3000:8185 4000:8189 5000:16369 6000:16377 7000:16381 8000:16381 9000:32737 10000:32753 20000:65521 30000:65533 40000:131057 50000:131069 60000:131069 70000:262113 80000:262129 90000:262137 100000:262141 200000:524285 300000:1048561 400000:1048573 500000:1048573 600000:2097137 700000:2097145 800000:2097149 900000:2097149 1000000:2097149 2000000:4194301 3000000:8388601 4000000:8388605 5000000:16777201 6000000:16777209 7000000:16777213 8000000:16777213 9000000:33554401 10000000:33554417?
?
?