Matlab兑现线性回归和逻辑回归: Linear Regression & Logistic Regression

Matlab实现线性回归和逻辑回归: Linear Regression & Logistic Regression
本文为Maching Learning 栏目补充内容，为上几章中所提到单参数线性回归、多参数线性回归和 逻辑回归的总结版。旨在帮助大家更好地理解回归，所以我在Matlab中分别对他们予以实现，在本文中由易到难地逐个介绍。

本讲内容：

Matlab 实现各种回归函数

=========================

基本模型

Y=θ0+θ1X1型---线性回归（直线拟合）

解决过拟合问题---Regularization

Y=1/(1+e^X)型---逻辑回归（sigmod 函数拟合）

=========================

第一部分：基本模型

在解决拟合问题的解决之前，我们首先回忆一下线性回归和逻辑回归的基本模型。

设待拟合参数 θn*1 和输入参数[ xm*n, ym*1 ] 。

对于各类拟合我们都要根据梯度下降的算法，给出两部分：

①   cost function（指出真实值y与拟合值h<hypothesis>之间的距离）：给出cost function 的表达式，每次迭代保证cost function的量减小；给出梯度gradient，即cost function对每一个参数θ的求导结果。

function [ jVal,gradient ] = costFunction ( theta )

 

②   Gradient_descent（主函数）：用来运行梯度下降算法，调用上面的cost function进行不断迭代，直到最大迭代次数达到给定标准或者cost function返回值不再减小。

function [optTheta,functionVal,exitFlag]=Gradient_descent( )

 

线性回归：拟合方程为hθ(x)=θ0x0+θ1x1+…+θnxn，当然也可以有xn的幂次方作为线性回归项（如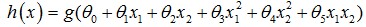），这与普通意义上的线性不同，而是类似多项式的概念。

其cost function 为：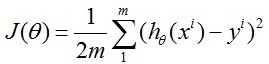

 

逻辑回归：拟合方程为hθ(x)=1/(1+e^(θTx))，其cost function 为：

 

cost function对各θj的求导请自行求取，看第三章最后一图，或者参见后文代码。

后面，我们分别对几个模型方程进行拟合，给出代码，并用matlab中的fit函数进行验证。

第二部分：Y=θ0+θ1X1型---线性回归（直线拟合）

在Matlab 线性拟合 & 非线性拟合中我们已经讲过如何用matlab自带函数fit进行直线和曲线的拟合，非常实用。而这里我们是进行ML课程的学习，因此研究如何利用前面讲到的梯度下降法（gradient descent）进行拟合。

cost function：

function PlotFunc( xstart,xend )%PLOTFUNC Summary of this function goes here%   draw original data and the fitted %===================cost function 2====linear regression%original datax1=[1;2;3;4];y1=[1.1;2.2;2.7;3.8];%plot(x1,y1,'ro-','MarkerSize',10);plot(x1,y1,'rx','MarkerSize',10);hold on;%fitted line - 拟合曲线x_co=xstart:0.1:xend;y_co=0.3+0.86*x_co;%plot(x_co,y_co,'g');plot(x_co,y_co);hold off;end

第三部分：解决过拟合问题---Regularization
过拟合问题解决方法我们已在第三章中讲过，利用Regularization的方法就是在cost function中加入关于θ的项，使得部分θ的值偏小，从而达到fit效果。例如定义costfunction J(θ)： jVal=(theta(1)-5)^2+(theta(2)-5)^2;

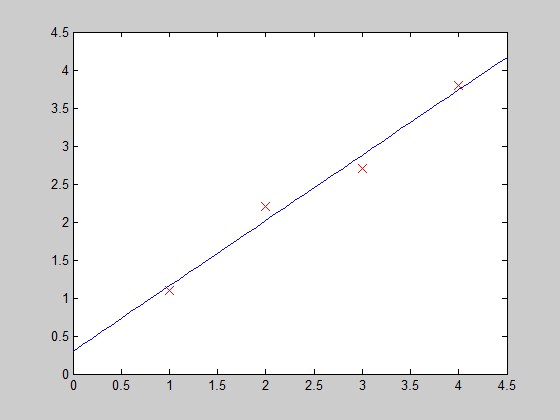
在每次迭代中，按照gradient descent的方法更新参数θ：θ(i)-=gradient(i),其中gradient(i)是J(θ)对θi求导的函数式，在此例中就有gradient(1)=2*(theta(1)-5), gradient(2)=2*(theta(2)-5)。

函数costFunction, 定义jVal=J(θ)和对两个θ的gradient：

==============================

Reference:
1. http://blog.csdn.net/abcjennifer/article/details/76915712.http://blog.csdn.net/abcjennifer/article/details/77007723.http://blog.csdn.net/abcjennifer/article/details/77162814.http://blog.csdn.net/abcjennifer/article/details/7684836

 

 

查看更多 下一篇