以求医为例谈搜索引擎排序算法的基础原理
我们向搜索引擎提交一个查询,搜索引擎会从先到后列出大量的结果,这些结果排序的标准是什么呢?这个看似简单的问题,却是信息检索专家们研究的核心难题之一。
为了说明这个问题,我们来研究一个比搜索引擎更加古老的话题:求医。比如,如果我牙疼,应该去看怎样的医生呢?假设我只有三种选择:
A医生肯定不在考虑之列。B医生和C医生之间,貌视更应该选择C医生,因为他更专注,更适合我的病情。假如再加一个条件:B医生经验丰富,有二十年从医经历,医术高明,而C医生只有五年从医经验,这个问题就不那么容易判断了,是优先选择更加专注的C医生,还是优先选择医术更加高明的B医生,的确成了一个需要仔细权衡的问题。
至少,我们得到了一个结论,择医需要考虑两个条件:医生的专长与病情的适配程度;医生的医术。大家肯定觉得这个结论理所当然,而且可以很自然地联想到,搜索引擎排序不也是这样吗,既要考虑网页内容与用户查询的匹配程度,又要考虑网页本身的质量。但是,怎么把这两种因素结合起来,得到一个,而不是两个或多个排序标准呢?假如我们把这两种因素表示成数值,最终的排序依据是把这两个数值加起来,还是乘起来,或是按决策树的办法把它们组织起来?如果是加起来,是简单相加,还是带权重加呢?
我们可以根据直觉和经验,通过试错的办法,把这两个因素结合起来。但更好的办法是我们能找到一个明确的依据,最好能跟数学这样坚实的学科联系起来。说起来,依据朴素的经验,人类在古代就能建造出高楼;但要建造出高达数百米的 摩天大厦,如果没有建筑力学、材料力学这样坚实的学科作为后盾,则是非常非常困难的。同理,依据朴素的经验构建的搜索引擎算法,用来处理上万的网页集合应该是没问题的;但要检索上亿的网页,则需要更为牢固的理论基础。
求医,病人会优先选择诊断准确、治疗效果好的医生;对于搜索引擎来说,一般按网页满足用户需求的概率从大到小排序。如果用q表示用户给出了一个特定的查询,用d表示一个特定的网页满足了用户的需求,那么排序的依据可以用一个条件概率来表示:
P(d|q)
这个简单的条件概率,将搜索引擎排序算法与概率论这门坚实的学科联系了起来,这就像在大海中航行的船只装备了指南针一样。利用贝叶斯公式,这个条件概率可以表示为:
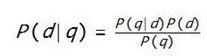
可以清楚地看到,搜索引擎的排序标准,是由三个部分组成的:查询本身的属性P(q);网页本身的属性P(d);两者的匹配关系P(q|d)。对于同一次查询来说,所有网页对应的P(q)都是一样的,因此排序时可以不考虑,即
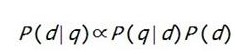
公式左边,是已知用户的查询,求网页满足该用户需求的概率。搜索引擎为了提高响应用户查询的性能,需要事先对所有待查询的网页做预处理。预处理时,只知道网页,不知道用户查询,因此需要倒过来计算,即分析每个网页能满足哪些需求,该网页分了多大比例来满足该需求,即得到公式右边的第一项P(q|d),这相当于上文介绍的医生的专门程度。比如,一个网页专门介绍牙病,另一个网页既介绍牙病又介绍胃病,那么对于“牙疼”这个查询来说,前一个网页的P(q|d)值就会更高一些。
公式右边的第二项P(d),是一个网页满足用户需求的概率,它反映了网页本身的好坏,与查询无关。假如要向一个陌生人推荐网页(我们并不知道他需要什么),那么P(d)就相当于某个特定的网页被推荐的概率。在传统的信息检索模型中,这一个量不太被重视,如传统的向量空间模型、BM25模型,都试图只根据查询与文档的匹配关系来得到排序的权重。而实际上,这个与查询无关的量是非常重要的。假如我们用网页被访问的频次来估计它满足用户需求的概率,可以看出对于两个不同的网页,这个量有着极其巨大的差异:有的网页每天只被访问一两次,而有的网页每天被访问成千上万次。能够提供如此巨大差异的量,竟长期被传统的搜索引擎忽略,直到Google发明了pagerank并让它参与到排序中。Pagerank是对P(d)值的一个不错的估计,这个因素的加入使搜索引擎的效果立即上升到了一个新的台阶。
这个公式同样回答了上文提出的问题,网页与查询的匹配程度,和网页本身的好坏,这两个因素应该怎样结合起来参与排序。这个公式以不可辩驳的理由告诉我们,如果网页与查询的匹配程度用P(q|d)来表示,网页本身的好坏用P(d)来表示,那么应该按它们的乘积来进行排序。在现代商业搜索引擎中,需要考虑更多更细节的排序因素,这些因素可能有成百上千个,要把它们融合起来是更加复杂和困难的问题。
来源:百度搜索研发部。