图像的几何形变与叠加
有时候,我们会遇到这样的需求:我们有两张图,一张图的场景包含在另一幅图中,但是我们不能直接做场景覆盖。
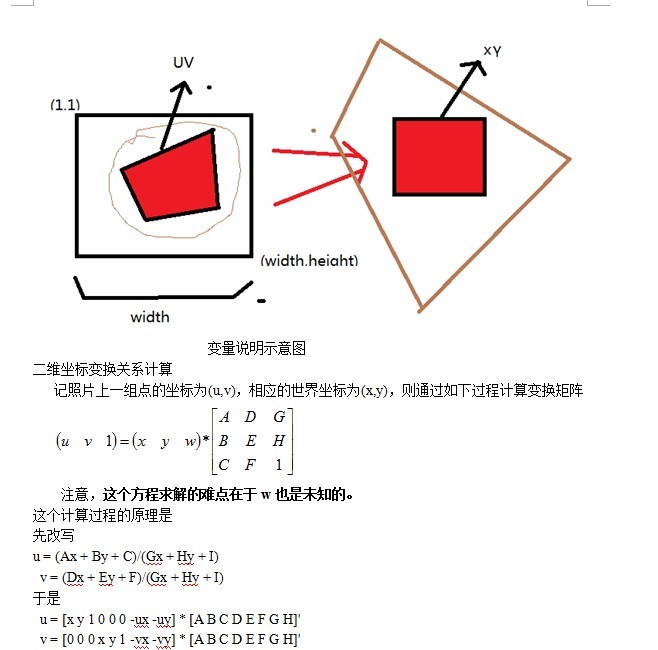
下图来自谷歌街景


为了做这样的拼接,需要对小图做一个几何变换。如下图所示。但前提是小图和大图的一系列对应点要已知才行。
计算过程如下。我分别给出了matlab程序和C语言程序。


#define N 8#include <math.h>void GetTransfMat(float uv[4][2],float xy[4][2],double mat[3][3]);void Array_Multipy43(double a[4][3], double b[3][3], double ab_multipy43[4][3]);int InverseMatrix(double *matrix,const int &row);void swap(double &a,double &b);//8*8的矩阵乘以列向量void Array_Multipy81(double a[][8], double b[], double ab_multipy81[]);void GetOuterCorner(int width,int height,double mat[3][3],double ab_multipy43[4][3]); //计算外边框在变换以后的坐标//4*3矩阵与3*3矩阵相乘void Array_Multipy43(double a[4][3], double b[3][3], double ab_multipy43[4][3]){int i,j,t;double temp = 0;int a1 = 4, a2 = 3, b2 = 3;//数组维数for(i = 0; i < a1; i++){for(j = 0; j < b2; j++){temp = 0; for(t = 0; t < a2; t++){ temp += a[i][t] * b[t][j]; } ab_multipy43[i][j] = temp; } } }void swap(double &a,double &b){double temp=a;a=b;b=temp;}/***********************************************函数名:InverseMatrix *函数介绍:求逆矩阵(高斯—约当法) *输入参数:矩阵首地址(二维数组)matrix,阶数row*输出参数:matrix原矩阵的逆矩阵*返回值:成功,0;失败,1*调用函数:swap(double &a,double &b)**********************************************/int InverseMatrix(double *matrix,const int &row){double *m=new double[row*row];double *ptemp,*pt=m;int i,j;ptemp=matrix;for (i=0;i<row;i++){ for (j=0;j<row;j++) { *pt=*ptemp; ptemp++; pt++; }}int k;int *is=new int[row],*js=new int[row];for (k=0;k<row;k++){ double max=0; //全选主元 //寻找最大元素 for (i=k;i<row;i++) { for (j=k;j<row;j++) { if (fabs(*(m+i*row+j))>max) { max=*(m+i*row+j); is[k]=i; js[k]=j; } } } if (0 == max) { return 1; } //行交换 if (is[k]!=k) { for (i=0;i<row;i++) { swap(*(m+k*row+i),*(m+is[k]*row+i)); } } //列交换 if (js[k]!=k) { for (i=0;i<row;i++) { swap(*(m+i*row+k),*(m+i*row+js[k])); } } *(m+k*row+k)=1/(*(m+k*row+k)); for (j=0;j<row;j++) { if (j!=k) { *(m+k*row+j)*=*((m+k*row+k)); } } for (i=0;i<row;i++) { if (i!=k) { for (j=0;j<row;j++) { if(j!=k) { *(m+i*row+j)-=*(m+i*row+k)**(m+k*row+j); } } } } for (i=0;i<row;i++) { if(i!=k) { *(m+i*row+k)*=-(*(m+k*row+k)); } }}int r;//恢复for (r=row-1;r>=0;r--){ if (js[r]!=r) { for (j=0;j<row;j++) { swap(*(m+r*row+j),*(m+js[r]*row+j)); } } if (is[r]!=r) { for (i=0;i<row;i++) { swap(*(m+i*row+r),*(m+i*row+is[r])); } }}ptemp=matrix;pt=m;for (i=0;i<row;i++){ for (j=0;j<row;j++) { *ptemp=*pt; ptemp++; pt++; }}delete []is;delete []js;delete []m;return 0;}//8*8的矩阵乘以列向量void Array_Multipy81(double a[][8], double b[], double ab_multipy81[]){int i,j,t;double temp = 0;int a1 = 8, a2 = 8;//数组维数for(i = 0; i < a1; i++){temp = 0; for(t = 0; t < a2; t++){ temp += a[i][t] * b[t]; } ab_multipy81[i] = temp; } }void GetTransfMat(float uv[4][2],float xy[4][2],double mat[3][3]) //计算变换矩阵{double vec_1[4][1];double vec_0[4][1];double U[8];for(int j=0;j<2;j++)for(int i=0;i<4;i++)U[4*j+i]=uv[i][j];double X[8][8];for(int i=0;i<4;i++){X[i][0]=xy[i][0];X[i][1]=xy[i][1];X[i][2]=1;X[i][3]=0;X[i][4]=0;X[i][5]=0;X[i][6]=-uv[i][0]*xy[i][0];X[i][7]=-uv[i][0]*xy[i][1];}for(int i=0;i<4;i++){X[i+4][0]=0;X[i+4][1]=0;X[i+4][2]=0;X[i+4][3]=xy[i][0];X[i+4][4]=xy[i][1];X[i+4][5]=1;X[i+4][6]=-uv[i][1]*xy[i][0];X[i+4][7]=-uv[i][1]*xy[i][1];}double x[N+1]={0};double *result=(double *)X;const int row=8; InverseMatrix(result,row);double a[N][N];for(int i=0;i<N;i++)for(int j=0;j<N;j++)a[i][j]= *(result+N*i+j);//8*8的矩阵乘以列向量Array_Multipy81(a,U,x);//free(result); x[N]=1;double Tinv[3][3]; for(int i=0;i<3;i++) for(int j=0;j<3;j++) Tinv[j][i]=x[3*i+j]; double *pmat=(double *)Tinv; const int row2=3; InverseMatrix(pmat,row2); for(int i=0;i<3;i++)for(int j=0;j<3;j++)mat[i][j]= *(pmat+3*i+j);}void GetOuterCorner(int width,int height,double mat[3][3],double ab_multipy43[4][3]) //计算外边框在变换以后的坐标{double corner[4][3];corner[0][0]=1; corner[0][1]=1;corner[1][0]=1; corner[1][1]=width; corner[2][0]=height; corner[2][1]=width;corner[3][0]=height; corner[3][1]=1; corner[3][2]=1;corner[2][2]=1;corner[1][2]=1;corner[0][2]=1;Array_Multipy43(corner, mat, ab_multipy43);for(int i=0;i<4;i++) for(int j=0;j<3;j++) ab_multipy43[i][j]=ab_multipy43[i][j]/ab_multipy43[i][2];}int _tmain(int argc, _TCHAR* argv[]){float uv[4][2]={{715.5665,367.2446},{856.4483,359.0450},{858.0231,441.7472},{700.4929,450.4702}};float xy[4][2]={{69.7741,167.1287},{309.2727,163.8221},{317.0277,289.0675},{43.5100,296.0256}}; double mat[3][3]={0}; int width=1276; int height=677;GetTransfMat(uv,xy,mat); double ab_multipy43[4][3]; GetOuterCorner( width, height,mat,ab_multipy43);//这里的ab_multipy43是一个4行3列的数组,4行分别对应外边界的四个角变形后的坐标 return 0;}