Stanford机器学习---第五讲. 神经网络的学习 Neural Networks learning
本栏目(Machine learning)包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM(Support Vector Machines 支持向量机)、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew老师的讲解。(https://class.coursera.org/ml/class/index)
第五讲——Neural Networks 神经网络的表示
===============================
Cost function
Backpropagation algorithm
Backpropagation intuition
Implementation note: Unrolling parameters
Gradient checking
Random initialization
Putting it together
===============================
Cost function
假设神经网络的训练样本有m个,每个包含一组输入x和一组输出信号y,L表示神经网络层数,Sl表示每层的neuron个数(SL表示输出层神经元个数)。
将神经网络的分类定义为两种情况:二类分类和多类分类,
卐二类分类:SL=1, y=0 or 1表示哪一类;
卐K类分类:SL=K, yi = 1表示分到第i类;(K>2)
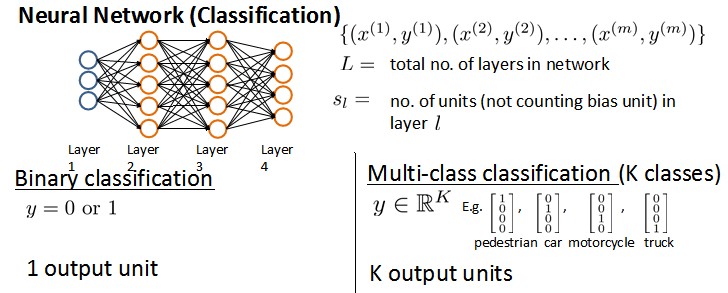
我们在前几章中已经知道,Logistic hypothesis的Cost Function如下定义:
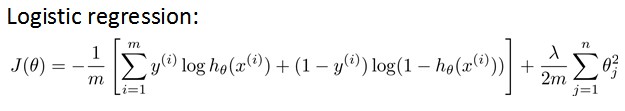
其中,前半部分表示hypothesis与真实值之间的距离,后半部分为对参数进行regularization的bias项,神经网络的cost function同理:
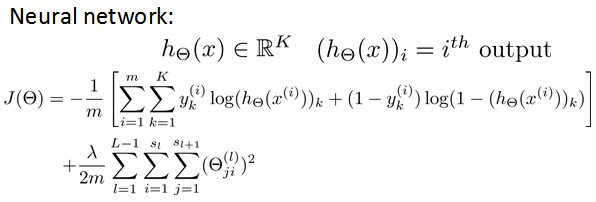
hypothesis与真实值之间的距离为 每个样本-每个类输出 的加和,对参数进行regularization的bias项处理所有参数的平方和
===============================
Backpropagation algorithm
前面我们已经讲了cost function的形式,下面我们需要的就是最小化J(Θ)

想要根据gradient descent的方法进行参数optimization,首先需要得到cost function和一些参数的表示。根据forward propagation,我们首先进行training dataset 在神经网络上的各层输出值:
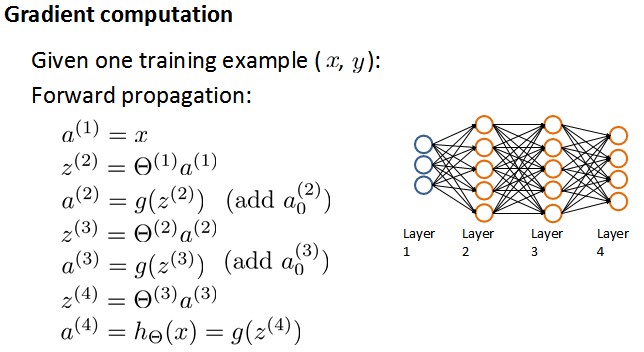
然后根据backpropagation算法进行梯度的计算,这里引入了error变量δ,用来表示真实值与forward propagation计算值之间的差,也是梯度的主要依据来源。
假设一个共有4层的神经网络,在最后一层,δ(4)= a(4)-y,而前面每一层的δ(j)由后一层传过来的δ(j+1)与上一层参数的积和g'(z(j))的点积决定(公式见下图)。对于公式
δ(j)=(Θ(j))Tδ(j+1) .* g'(z(j))
g'(z(j))=a(j).*(1-a(j)),
其中 z(j)和a(j)都是列向量,1表示一列1向量。

由上图我们得到了error变量δ的计算,下面我们来看backpropagation算法的伪代码:

ps:最后一步之所以写+=而非直接赋值是把Δ看做了一个矩阵,每次在相应位置上做修改。
从后向前此计算每层依的δ,用Δ表示全局误差,每一层都对应一个Δ(l)。再引入D作为cost function对参数的求导结果。下图左边j是否等于0影响的是是否有最后的bias regularization项。左边是定义,右边可证明(比较繁琐)。

===============================
Backpropagation intuition
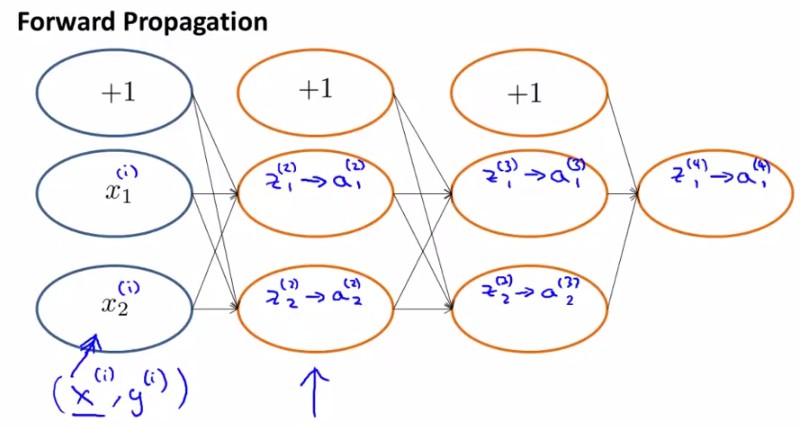
上面讲了backpropagation算法的步骤以及一些公式,在这一小节中我们讲一下最简单的back-propagation模型是怎样learning的。首先根据forward propagation方法从前往后计算z(j),a(j) ;
然后将原cost function 进行简化,去掉下图中后面那项regularization项,
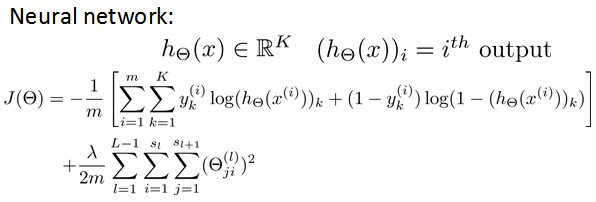
那么对于输入的第i个样本(xi,yi),有
Cost(i)=y(i)log(hθ(x(i)))+(1- y(i))log(1- hθ(x(i)))
那么对于error分量,有
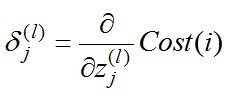
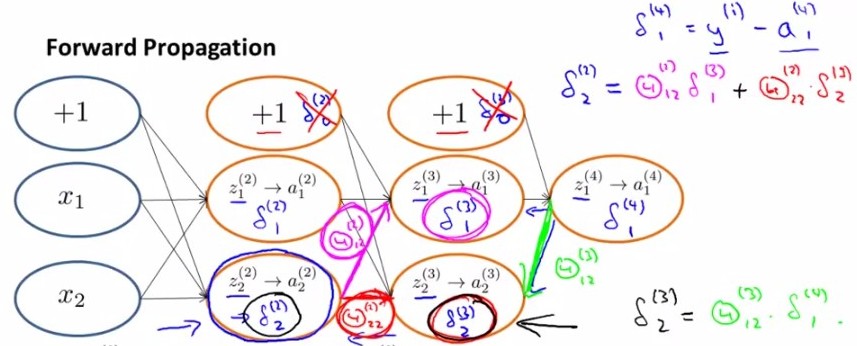
经过求导计算可得,对于上图有
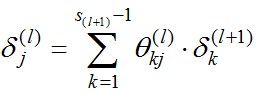
换句话说, 对于每一层来说,δ分量都等于后面一层所有的δ加权和,其中权值就是参数Θ。
===============================
Implementation note: Unrolling parameters
这一节讲述matlab中如何实现unrolling parameter。
前几章中已经讲过在matlab中利用梯度下降方法进行更新的根本,两个方程:
function [jVal, gradient] = costFunction(theta)optTheta = fminunc(@costFunction, initialTheta, options)与linear regression和logistic regression不同,在神经网络中,参数非常多,每一层j有一个参数向量Θj和Derivative向量Dj。那么我们首先将各层向量连起来,组成大vectorΘ和D,传入function,再在计算中进行下图中的reshape,分别取出进行计算。

计算时,方法如下:

===============================
Gradient checking
神经网络中计算起来数字千变万化难以掌握,那我们怎么知道它里头工作的对不对呢?不怕,我们有法宝,就是gradient checking,通过check梯度判断我们的code有没有问题,ok?怎么做呢,看下边:
对于下面这个【Θ-J(Θ)】图,取Θ点左右各一点(Θ+ε),(Θ-ε),则有点Θ的导数(梯度)近似等于(J(Θ+ε)-J(Θ-ε))/(2ε)。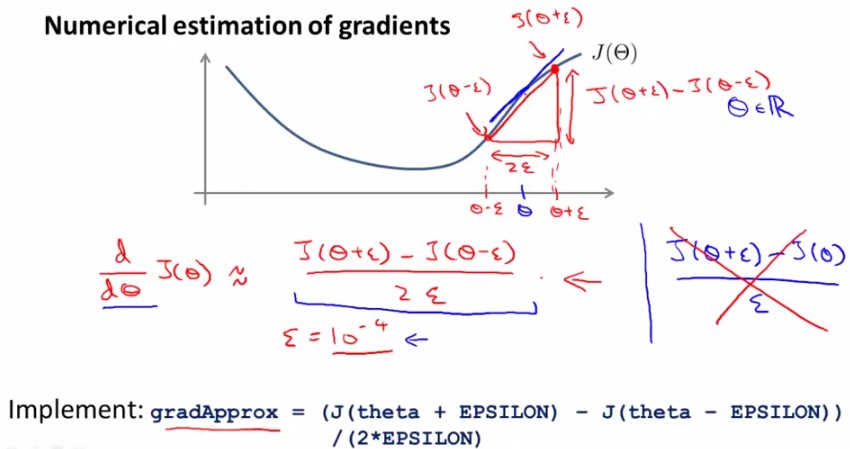
对于每个参数的求导公式如下图所示:

由于在back-propagation算法中我们一直能得到J(Θ)的导数D(derivative),那么就可以将这个近似值与D进行比较,如果这两个结果相近就说明code正确,否则错误,如下图所示:

Summary: 有以下几点需要注意
-在back propagation中计算出J(θ)对θ的导数D,并组成vector(Dvec)
-用numerical gradient check方法计算大概的梯度gradApprox=(J(Θ+ε)-J(Θ-ε))/(2ε)
-看是否得到相同(or相近)的结果
-(这一点非常重要)停止check,只用back propagation 来进行神经网络学习(否则会非常慢,相当慢)

===============================
Random Initialization
对于参数θ的initialization问题,我们之前采用全部赋0的方法,比如:
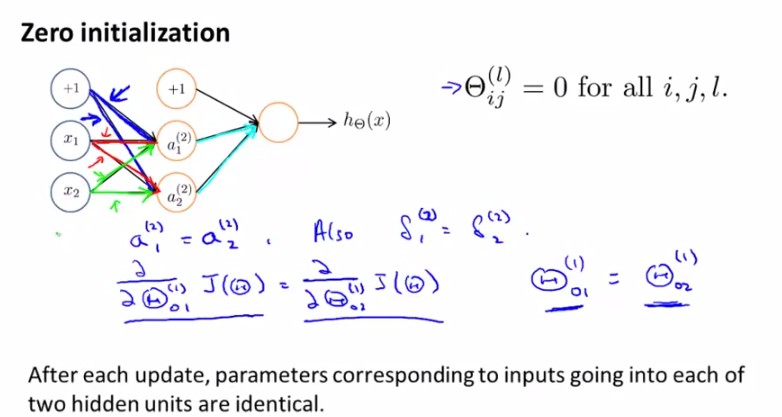
所以我们应该打破这种symmetry,randomly选取每一个parameter,在[-ε,ε]范围内:

===============================
Putting it together
1. 选择神经网络结构
我们有很多choices of network :
那么怎么选择呢?
No. of input units: Dimension of features
No. output units: Number of classes
Reasonable default: 1 hidden layer, or if >1 hidden layer, have same no. of hidden units in every layer (usually the more the better)
2. 神经网络的训练
① Randomly initialize weights
② Implement forward propagation to get hθ(x(i)) for any x(i)
③ Implement code to compute cost function J(θ)
④ Implement backprop to compute partial derivatives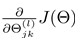

⑤

⑥

test:

本章讲述了神经网络学习的过程,重点在于back-propagation算法,gradient-checking方法,希望能够有人用我之前这篇文章中的类似方法予以实现神经网络。
关于Machine Learning更多的学习资料将继续更新,敬请关注本博客和新浪微博Sophia_qing。