回溯算法---四色图着色
回溯算法基本思想:
判断第一个节点的各个候选值{ //当无未进行判断的候选者时,则退出
当将某候选值赋予第一个节点时,判断此时是否存在一个解路径。
若不存在,则继续判断下一个候选值。
}
具体算法思想如下:
NUM : 解路径上节点的个数
CANDIDATA_NUM: 每个节点的候选值的个数
BOOL TestNode(I,j)
判断当将候选值j赋予节点i时,是否能找到一条解路径
//是否有解
BOOL Find()
{
BOOL bExist=FALSE;
//从起始节点的候选值依次判断
For(int j=0; j<CANDIDATA_NUM;j++)
{
IF(TestNode(0,j))
{
bExist=True;
}
}
Return bExist;
}
四色图问题:
设有下图所示地图,每个区域代表一个省,区域中的数字代表省的编号,今将每个省涂上红(R),兰(B),黄(Y),绿(G)四种颜色之一,使相邻的省份有不同的颜色。
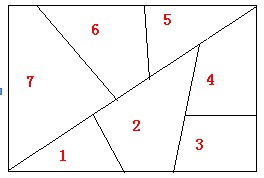
算法说明:
这是一道非常典型的回溯题目。解法与“八皇后问题”一样。在填写每一个省的颜色时检查与相邻已填省份的颜色是否相同。如果不同,则填上;如果相同(冲突),则另选一种;如果已没有颜色可供选择,则回溯到上一省份。重复这一过程,直到所有省的颜色都已填上。
最主要的问题在于如何解决相邻省的颜色冲突。对每一个省份,可供选择的颜色一共有四种;对省份i来说颜色x可填的条件是编号为1~(i-1)且与省i相邻的省份的颜色都不是x。
各省之间的相邻关系用矩阵R(n,n)来表示:
r(i,j)=1或0 1:表示相邻 0表示不相邻
本题的相邻矩阵如下:
0
1
0
0
0
0
1
1
0
1
1
1
1
1
0
1
0
1
0
0
0
1
1
1
0
1
0
0
0
1
0
1
0
1
0
0
1
0
0
1
0
1
1
1
0
0
0
1
0
主要函数:
经测试,此图共有192中着色方案, 示例如下:



测试程序:
http://download.csdn.net/detail/shuilan0066/4406160