在公务员考试的行政职业能力测验中，数学运算一直是重头戏，而数学运算中有许多问题都有着一定的难度，使得一些考生望而却步。下面讨论的排列组合问题就是难点之一。当然，万变不离其宗，掌握问题本质，再难的问题都可以迎刃而解。为帮助考生掌握快速答题技巧，华图教研中心公务员考试辅导专家王永恒老师结合多年辅导经验，向考生们介绍一个比较常见也非常有效的解决排列组合问题的方法：插板法。
插板法是用于解决“相同元素”分组问题，且要求每组均“非空”，即要求每组至少一个元素；若对于 “可空”问题，即每组可以是零个元素，又该如何解题呢？
下面先给各位考生看一道题目：
例1．现有10个完全相同的球全部分给7个班级，每班至少1个球，问共有多少种不同的分法?
【解析】题目中球的分法共三类：
第一类：有3个班每个班分到2个球，其余4个班每班分到1个球。其分法种数为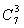
。
第二类：有1个班分到3个球，1个班分到2个球，其余5个班每班分到1个球。其分法种数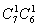
。
第三类：有1个班分到4个球，其余的6个班每班分到1个球。其分法种数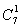
。
所以，10个球分给7个班，每班至少一个球的分法种数为：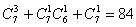
。
从上面解题过程来看，对这类问题进行分类计算，比较繁琐，若是上题中球的数目较多处理起来将更加困难，因此我们需要寻求一种新的模式解决问题，我们创设这样一种虚拟的情境——插板。
将10个相同的球排成一行，10个球之间出现了9个空档，现在我们用“挡板”把10个球隔成有序的7份，每个班级依次按班级序号分到对应位置的几个球（可能是1个、2个、3个、4个），借助于这样的虚拟“挡板”分配物品的方法称之为插板法。
由上述分析可知，分球的方法实际上为挡板的插法：即是在9个空档之中插入6个“挡板”（6个挡板可把球分为7组），其方法种数为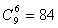
。
由上述问题的分析可看到，这种插板法解决起来非常简单，但同时也提醒各位考生，这类问题模型的适用前提相当严格，必须同时满足以下3个条件：
①所要分的元素必须完全相同；
②所要分的元素必须分完，决不允许有剩余；
③参与分元素的每组至少分到1个，决不允许出现分不到元素的组。
下面再给各位看一道例题：
例2．有8个相同的球放到三个不同的盒子里，共有（ ）种不同方法.
A．35 B．28 C．21 D．45
【解析】这道题很多同学错选C，错误的原因是直接套用上面所讲的“插板法”，而忽略了“插板法”的适用条件。例2和例1的最大区别是：例1的每组元素都要求“非空”，而例2则无此要求，即可以出现空盒子。
其实此题还是用“插板法”，只是要做一些小变化，详解如下：
 |
设想把这8个球一个接一个排起来，即 ，共形成9个空档（此时的空档包括中间7个空档和两端2个空档），然后用2个挡板把这8个球分成3组，先插第一个挡板，由于可以有空盒，所以有9个空档可以插；再插第二个板，有10个空档可以插，但由于两个板是不可分的（也就是说当两个挡板相邻时，虽然是两种插法，但实际上是一种分法），所以共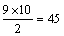
种。
例3．（1）已知方程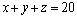
，求这个方程的正整数解的个数。
（2）已知方程，求这个方程的非负整数解的个数。
【解析】(1)将20分成20个1，列出来：1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1在这20个数中间的19个空中插入2个板子，将20分成3部分，每一部分对应“1”的个数，按顺序排成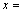
；
；
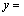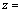；即是正整数解。故正整数解的个数为
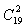，解法非常简单。
（2）此题和例2的解法完全相同，请各位考生自己考虑一下。
从以上例题的分析来看，在利用“插板法”解决这种相同元素排列组合问题时，一定要注意“空”与“不空”的分析，防止掉入陷阱。例3的两题相比较，可以很明显地看出“空”与“不空”的区别。
“非空”问题插板法题目原型为：设有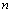
个相同元素，分成
（
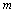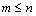）组，每组至少一个元素的分组方法共有
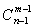；“可空”问题插板法问题原型为：设有个相同元素，分成（）组，则分组方法共有
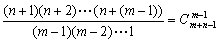种方法（对于“可空”问题，只要记住公式即可，不要求掌握原理）。
练习：有10级台阶，分8步走完。每步可以迈1级、2级或3级台阶，有多少种走法？（答案为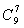
）
老子曰：夫物芸芸，各复归其根，归根曰静，静曰复命。在考生平时的学习中，应当学会寻找共性，寻找根源，从本质上理解归纳各种问题，这样才能准确把握问题的突破口，提高解决问题的能力。祝各位考生备考顺利，在国考中取得理想的成绩！
